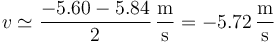Entrar Página Discusión Historial Go to the site toolbox

Análisis numérico de movimiento

De Laplace

(Diferencias entre revisiones)
Línea 6: Línea 6:
! t (s)
! t (s)
| 0.0  
| 0.0  
-
| 1.0  
+
| 0.1
-
| 2.0  
+
| 0.2
-
| 3.0  
+
| 0.3
-
| 4.0  
+
| 0.4
-
| 5.0  
+
| 0.5
-
| 6.0
+
| 0.6
|-
|-
! x (m)
! x (m)
Línea 27: Línea 27:
|-
|-
! t (s)
! t (s)
-
| 7.0  
+
| 0.7
-
| 8.0
+
| 0.8  
-
| 9.0
+
| 0.9  
-
| 10.0  
+
| 1.0  
-
| 11.0
+
| 1.1
-
| 12.0
+
| 1.2
-
| 13.0
+
| 1.3
|-
|-
! x (m)
! x (m)
Línea 49: Línea 49:
|-
|-
! t (s)
! t (s)
-
| 14.0
+
| 1.4
-
| 15.0
+
| 1.5
-
| 16.0
+
| 1.6
-
| 17.0
+
| 1.7
-
| 18.0
+
| 1.8
-
| 19.0
+
| 1.9
-
| 20.0
+
| 2.0
|-
|-
! x (m)
! x (m)
Línea 69: Línea 69:
Para este movimiento, halle:
Para este movimiento, halle:
-
# El desplazamiento entre <math>t = 0.0\,\mathrm{s}</math> y <math>t=20.0\,\mathrm{s}</math>, así como el valor aproximado de la distancia recorrida en dicho intervalo.
+
# El desplazamiento entre <math>t = 0.0\,\mathrm{s}</math> y <math>t=2.0\,\mathrm{s}</math>, así como el valor aproximado de la distancia recorrida en dicho intervalo.
# La velocidad media y la rapidez media en el intervalo anterior.  
# La velocidad media y la rapidez media en el intervalo anterior.  
-
# La velocidad media en los intervalos (0.0s, 6.0s), (2.0s, 11.0s) y (6.0s, 15.0s).
+
# La velocidad media en los intervalos (0.0s, 0.6s), (0.2s, 1.1s) y (0.6s, 1.5s).
-
# El valor aproximado de la velocidad en <math>t= 12.0\,\mathrm{s}</math>.
+
# El valor aproximado de la velocidad en <math>t= 1.2\,\mathrm{s}</math>.
-
# El valor aproximado de la aceleración en <math>t= 12.0\,\mathrm{s}</math>.
+
# El valor aproximado de la aceleración en <math>t= 1.2\,\mathrm{s}</math>.
# Sabiendo que este movimiento sigue una ley de la forma
# Sabiendo que este movimiento sigue una ley de la forma
Línea 81: Línea 81:
:# Los valores de las constantes <math>A_k</math>.
:# Los valores de las constantes <math>A_k</math>.
:# El valor exacto de la distancia recorrida y la rapidez media.
:# El valor exacto de la distancia recorrida y la rapidez media.
-
:# El valor exacto de la velocidad y de la aceleración en <math>t = 12.0\,\mathrm{s}</math>.
+
:# El valor exacto de la velocidad y de la aceleración en <math>t = 1.2\,\mathrm{s}</math>.
==Desplazamiento en el intervalo completo==
==Desplazamiento en el intervalo completo==
Línea 87: Línea 87:
El desplazamiento lo calculamos como la diferencia entre la posición final y la inicial
El desplazamiento lo calculamos como la diferencia entre la posición final y la inicial
-
<center><math>\Delta x = x(20.0\,\mathrm{s})-x(0.0\,\mathrm{s})=-3.328\,\mathrm{m}-(-1.728\,\mathrm{m})= -1.600\,\mathrm{m}</math></center>
+
<center><math>\Delta x = x(2.0\,\mathrm{s})-x(0.0\,\mathrm{s})=-3.328\,\mathrm{m}-(-1.728\,\mathrm{m})= -1.600\,\mathrm{m}</math></center>
Este desplazamiento corresponde gráficamente a la distancia vertical entre el punto inicial y el final.
Este desplazamiento corresponde gráficamente a la distancia vertical entre el punto inicial y el final.
<center>
<center>
-
[[Archivo:cubica-01.png]]</center>
+
[[Archivo:cubica-01.png|600px]]</center>
===Distancia recorrida===
===Distancia recorrida===
Línea 111: Línea 111:
La velocidad media la calculamos como el despalzamiento dividido por el intervalo de tiempo
La velocidad media la calculamos como el despalzamiento dividido por el intervalo de tiempo
-
<center><math>v_m=\frac{\Delta x}{\Delta t}=\frac{-1.600\,\mathrm{m}}{20.0\mathrm{s}}=-0.080\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+
<center><math>v_m=\frac{\Delta x}{\Delta t}=\frac{-1.600\,\mathrm{m}}{2.0\mathrm{s}}=-0.800\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
y la rapidez media se calcula de la misma forma pero con la distancia recorrida
y la rapidez media se calcula de la misma forma pero con la distancia recorrida
-
<center><math>|v|_m=\frac{\Delta s}{\Delta t}=\frac{9.376\,\mathrm{m}}{20.0\mathrm{s}}=0.469\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+
<center><math>|v|_m=\frac{\Delta s}{\Delta t}=\frac{9.376\,\mathrm{m}}{2.00\mathrm{s}}=4.688\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
==Velocidades medias==
==Velocidades medias==
Para cada uno de los tres intervalos se calcula la velocidad media como el cociente entre el desplzamiento y el intervalo. Resulta en el primer caso
Para cada uno de los tres intervalos se calcula la velocidad media como el cociente entre el desplzamiento y el intervalo. Resulta en el primer caso
-
<center><math>v_m=\frac{x_6-x_0}{6.0\,\mathrm{s}-0.0\,\mathrm{s}}= \frac{3.888\,\mathrm{m}}{6.0\,\mathrm{s}}= +0.648\,\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+
<center><math>v_m=\frac{x_6-x_0}{0.6\,\mathrm{s}-0.0\,\mathrm{s}}= \frac{3.888\,\mathrm{m}}{0.6\,\mathrm{s}}= +6.48\,\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
en el segundo
en el segundo
-
<center><math>v_m=\frac{x_11-x_2}{11.0\,\mathrm{s}-2.0\,\mathrm{s}}= \frac{0.000\,\mathrm{m}}{6.0\,\mathrm{s}}= 0.000\,\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+
<center><math>v_m=\frac{x_{11}-x_2}{1.1\,\mathrm{s}-0.2\,\mathrm{s}}= \frac{0.000\,\mathrm{m}}{0.9\,\mathrm{s}}= 0.000\,\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
y en el tercero
y en el tercero
-
<center><math>v_m=\frac{x_15-x_6}{15.0\,\mathrm{s}-6.0\,\mathrm{s}}= \frac{-3.888\,\mathrm{m}}{6.0\,\mathrm{s}}= -0.432\,\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+
<center><math>v_m=\frac{x_{15}-x_6}{1.5\,\mathrm{s}-0.6\,\mathrm{s}}= \frac{-3.888\,\mathrm{m}}{0.9\,\mathrm{s}}= -4.32\,\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
Vemos que la velocidad media puede tener cualquier signo o ser nula, dependiendo de hacia donde es el desplazamiento. En cada caso se trata de la pendiente de la secante que pasa por los dos instantes indicados.
Vemos que la velocidad media puede tener cualquier signo o ser nula, dependiendo de hacia donde es el desplazamiento. En cada caso se trata de la pendiente de la secante que pasa por los dos instantes indicados.
-
<center>[[Archivo:cubica-03.png]]</center>
+
<center>[[Archivo:cubica-03.png|600px]]</center>
==Velocidad instantánea==
==Velocidad instantánea==
 +
Para calcular la velocidad instantánea necesitamos hallar la derivada, lo cual no podemos hacer exactamente pues no disponemos de una función para derivar.
 +
 +
No obstante, si el intervalo de tiempo es pequeño, podemos aproximar la velocidad instantánea por la velocidad media en ese pequeño intervalo.
 +
 +
En este caso podemos tomar el intervalo (1.1s,1.2s) y el (1.2s,1.3s). En el primer caso obtenemos la aproximación
 +
 +
<center><math>v\simeq \frac{x_{12}-x_11}{1.2\,\mathrm{s}-1.1\,\mathrm{s}}= \frac{-0.560\,\mathrm{m}}{0.1\,\mathrm{s}}= -5.60\,\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
 +
y en el segundo
 +
 +
<center><math>v\simeq \frac{x_{13}-x_12}{1.3\,\mathrm{s}-1.2\,\mathrm{s}}= \frac{-0.584\,\mathrm{m}}{0.1\,\mathrm{s}}= -5.84\,\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
 +
Una mejor aproximación es la media de estos dos valores
 +
 +
<center><math>v\simeq \frac{-5.60-5.84}{2}\,\frac{\mathrm{m}}{\mathrm{s}}= -5.72\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
==Aceleración instantánea==
==Aceleración instantánea==
==Cálculos exactos==
==Cálculos exactos==
[[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]]
[[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]]

Revisión de 22:25 7 nov 2015

Contenido

1 Enunciado

La posición de una partícula en distintos instantes de tiempo es, aproximadamente

t (s) 0.0 0.1 0.2 0.3 0.4 0.5 0.6
x (m) −1.728 −0.440 0.560 1.296 1.792 2.072 2.160


t (s) 0.7 0.8 0.9 1.0 1.1 1.2 1.3
x (m) 2.080 1.856 1.512 1.072 0.560 0.000 −0.584


t (s) 1.4 1.5 1.6 1.7 1.8 1.9 2.0
x (m) −1.168 −1.728 −2.240 −2.680 −3.024 −3.248 −3.328

Para este movimiento, halle:

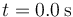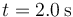  1. El desplazamiento entre t = 0.0\,\mathrm{s} y t=2.0\,\mathrm{s}, así como el valor aproximado de la distancia recorrida en dicho intervalo.
  2. La velocidad media y la rapidez media en el intervalo anterior.
  3. La velocidad media en los intervalos (0.0s, 0.6s), (0.2s, 1.1s) y (0.6s, 1.5s).
  4. El valor aproximado de la velocidad en t= 1.2\,\mathrm{s}.
  5. El valor aproximado de la aceleración en t= 1.2\,\mathrm{s}.
  6. Sabiendo que este movimiento sigue una ley de la forma
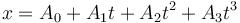
x = A_0 + A_1 t + A_2 t^2 + A_3 t^3\,
Calcule
  1. Los valores de las constantes Ak.
  2. El valor exacto de la distancia recorrida y la rapidez media.
  3. El valor exacto de la velocidad y de la aceleración en t = 1.2\,\mathrm{s}.

2 Desplazamiento en el intervalo completo

2.1 Desplazamiento

El desplazamiento lo calculamos como la diferencia entre la posición final y la inicial

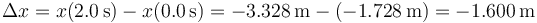
\Delta x = x(2.0\,\mathrm{s})-x(0.0\,\mathrm{s})=-3.328\,\mathrm{m}-(-1.728\,\mathrm{m})= -1.600\,\mathrm{m}

Este desplazamiento corresponde gráficamente a la distancia vertical entre el punto inicial y el final.

2.2 Distancia recorrida

Podemos hallar de forma aproximada la distancia recorrida sumando las diferencias entre posiciones, con valor absoluto.

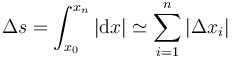
\Delta s = \int_{x_0}^{x_n} |\mathrm{d}x|\simeq \sum_{i=1}^{n} |\Delta x_i|

Para ello, construimos una tabla de diferencias y sumamos (con ayuda de un ordenador).

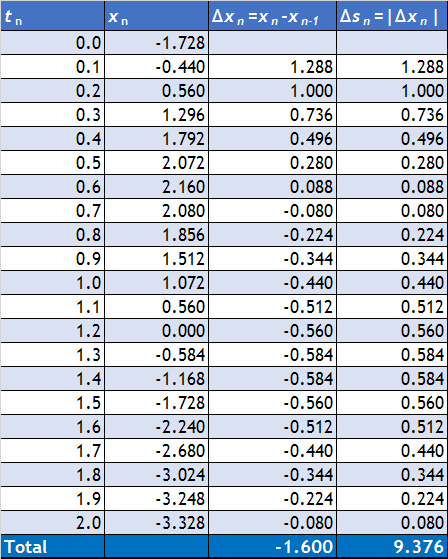
Archivo:cubica-02.png

Vemos que la distancia recorrida es de 9.376m.

Este procedimiento es general siempre que tengamos una tabla de valores. Sin embargo, para este caso podemos calcular la distancia recorrida por simple inspección. Vemos que la masa parte de un valor de x negativo va aumentando hasta un máximo y a partir de ahi retrocede hasta otro valor negativo. Podemos hallar la distancia total sumando lo que recorre en la ida con lo que recorre en la vuelta

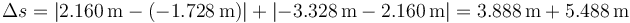
\Delta s = \left|2.160\,\mathrm{m}-(-1.728\,\mathrm{m})\right| + \left|-3.328\,\mathrm{m}-2.160\,\mathrm{m}\right|=3.888\,\mathrm{m}+5.488\,\mathrm{m}

3 Velocidad y rapidez media

La velocidad media la calculamos como el despalzamiento dividido por el intervalo de tiempo

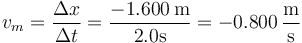
v_m=\frac{\Delta x}{\Delta t}=\frac{-1.600\,\mathrm{m}}{2.0\mathrm{s}}=-0.800\,\frac{\mathrm{m}}{\mathrm{s}}

y la rapidez media se calcula de la misma forma pero con la distancia recorrida

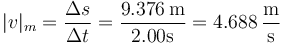
|v|_m=\frac{\Delta s}{\Delta t}=\frac{9.376\,\mathrm{m}}{2.00\mathrm{s}}=4.688\,\frac{\mathrm{m}}{\mathrm{s}}

4 Velocidades medias

Para cada uno de los tres intervalos se calcula la velocidad media como el cociente entre el desplzamiento y el intervalo. Resulta en el primer caso

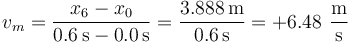
v_m=\frac{x_6-x_0}{0.6\,\mathrm{s}-0.0\,\mathrm{s}}= \frac{3.888\,\mathrm{m}}{0.6\,\mathrm{s}}= +6.48\,\,\frac{\mathrm{m}}{\mathrm{s}}

en el segundo

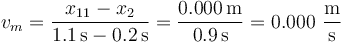
v_m=\frac{x_{11}-x_2}{1.1\,\mathrm{s}-0.2\,\mathrm{s}}= \frac{0.000\,\mathrm{m}}{0.9\,\mathrm{s}}= 0.000\,\,\frac{\mathrm{m}}{\mathrm{s}}

y en el tercero

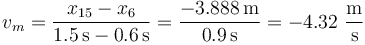
v_m=\frac{x_{15}-x_6}{1.5\,\mathrm{s}-0.6\,\mathrm{s}}= \frac{-3.888\,\mathrm{m}}{0.9\,\mathrm{s}}= -4.32\,\,\frac{\mathrm{m}}{\mathrm{s}}

Vemos que la velocidad media puede tener cualquier signo o ser nula, dependiendo de hacia donde es el desplazamiento. En cada caso se trata de la pendiente de la secante que pasa por los dos instantes indicados.

5 Velocidad instantánea

Para calcular la velocidad instantánea necesitamos hallar la derivada, lo cual no podemos hacer exactamente pues no disponemos de una función para derivar.

No obstante, si el intervalo de tiempo es pequeño, podemos aproximar la velocidad instantánea por la velocidad media en ese pequeño intervalo.

En este caso podemos tomar el intervalo (1.1s,1.2s) y el (1.2s,1.3s). En el primer caso obtenemos la aproximación

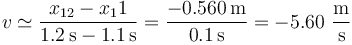
v\simeq \frac{x_{12}-x_11}{1.2\,\mathrm{s}-1.1\,\mathrm{s}}= \frac{-0.560\,\mathrm{m}}{0.1\,\mathrm{s}}= -5.60\,\,\frac{\mathrm{m}}{\mathrm{s}}

y en el segundo

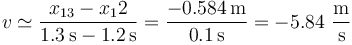
v\simeq \frac{x_{13}-x_12}{1.3\,\mathrm{s}-1.2\,\mathrm{s}}= \frac{-0.584\,\mathrm{m}}{0.1\,\mathrm{s}}= -5.84\,\,\frac{\mathrm{m}}{\mathrm{s}}

Una mejor aproximación es la media de estos dos valores

v\simeq \frac{-5.60-5.84}{2}\,\frac{\mathrm{m}}{\mathrm{s}}= -5.72\,\frac{\mathrm{m}}{\mathrm{s}}

6 Aceleración instantánea

7 Cálculos exactos

Obtenido de "http://tesla.us.es/wiki/index.php/An%C3%A1lisis_num%C3%A9rico_de_movimiento"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace