Rapidez de impacto

De Laplace

(Diferencias entre revisiones)

última version al 17:24 28 oct 2015

1 Enunciado

Una partícula está sometida exclusivamente a la acción de la gravedad. Si se lanza con velocidad $+ v 0$ en dirección vertical hacia arriba desde un punto de altura $h$ . ¿Cuál es su velocidad cuando llega al suelo? Si en vez de lanzarse hacia arriba se lanza hacia abajo, con velocidad $- v 0$ , ¿llegará con una rapidez mayor?

2 Solución

Este problema puede resolverse de diferentes maneras.

La partícula sigue un movimiento uniformemente acelerado en el que la aceleración es la de la gravedad. Las ecuaciones para la posición y la velocidad en función del tiempo son

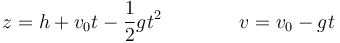
$z = h + v_0 t -\frac{1}{2}gt^2\qquad\qquad v = v_0-gt$

La condición de impacto la da el que la posición llegue a $z = 0$ . Esto conduce a una ecuación de segundo grado para $t$

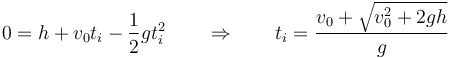
$0 = h + v_0 t_i -\frac{1}{2}gt_i^2 \qquad\Rightarrow\qquad t_i = \frac{v_0+\sqrt{v_0^2+2gh}}{g}$

donde hemos descartado la solución con el signo negativo, ya que conduce a un tiempo menor que cero. Llevando esto a la ecuación de la velocidad queda

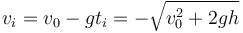
$v_i = v_0 - gt_i = -\sqrt{v_0^2+2gh}$

Resulta una velocidad negativa porque la partícula está descendiendo. La rapidez de impacto será

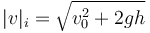
$|v|_i = \sqrt{v_0^2+2gh}$

Podemos ahorrarnos la resolución de la ecuación de segundo grado observando si elevamos al cuadrado la ecuación de la velocidad

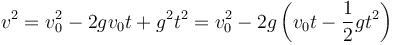
$v^2 = v_0^2 -2gv_0t + g^2 t^2 = v_0^2 - 2g\left(v_0t-\frac{1}{2}gt^2\right)$

pero lo que está entre paréntesis es $z - h$ , así que llegamos a la igualdad

$v^2 = v_0^2 -2g(z-h)$

que particularizada para el momento de impacto nos da

$v_i^2 = v_0^2 + 2gh\qquad\Rightarrow\qquad |v|_i=\sqrt{v_0^2+2gh}$

Este segundo procedimiento es un caso particular de la fórmula

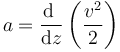
$a = \frac{\mathrm{d}\ }{\mathrm{d}z}\left(\frac{v^2}{2}\right)$

que para el caso de una aceleración constante equivale al cociente entre incrementos

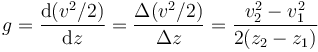
$g=\frac{\mathrm{d}(v^2/2) }{\mathrm{d}z}=\frac{\Delta(v^2/2)}{\Delta z}=\frac{v_2^2-v_1^2}{2(z_2-z_1)}$

cuyo resultado es inmediato

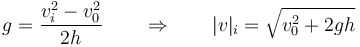
$g = \frac{v_i^2-v_0^2}{2h}\qquad\Rightarrow\qquad |v|_i=\sqrt{v_0^2 + 2gh}$

Vemos que el resultado es independiente del signo de $v 0$ . Por tanto, si la piedra es lanzada hacia arriba en vez de hacia abajo, el resultado es el mismo. Eso sí, la piedra que va hacia arriba tarda más en llegar al suelo.

@@ Línea 37: / Línea 37: @@
 <center><math>a = \frac{\mathrm{d}\ }{\mathrm{d}z}\left(\frac{v^2}{2}\right)</math></center>
-que integrada entre la posición inicial y la final nos da
+que para el caso de una aceleración constante equivale al cociente entre incrementos
-<center><math>\int_h^0 (-g)\mathrm{d}z = \int_{v_0}^{v_i}\mathrm{d}\left(\frac{v^2}{2}\right)</math></center>
+<center><math>g=\frac{\mathrm{d}(v^2/2) }{\mathrm{d}z}=\frac{\Delta(v^2/2)}{\Delta z}=\frac{v_2^2-v_1^2}{2(z_2-z_1)}</math></center>
 cuyo resultado es inmediato
-<center><math>gh = \frac{1}{2}v_i^2 -\frac{1}{2}v_0^2\qquad\Rightarrow\qquad |v|_i=\sqrt{v_0^2 + 2gh}</math></center>
+<center><math>g = \frac{v_i^2-v_0^2}{2h}\qquad\Rightarrow\qquad |v|_i=\sqrt{v_0^2 + 2gh}</math></center>
 Vemos que el resultado es independiente del signo de <math>v_0</math>. Por tanto, si la piedra es lanzada hacia arriba en vez de hacia abajo, el resultado es el mismo. Eso sí, la piedra que va hacia arriba tarda más en llegar al suelo.
 [[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]]

Rapidez de impacto

De Laplace

última version al 17:24 28 oct 2015

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES