1.1. Expresión que carece de sentido (Ex.Nov/12)
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
(→Enunciado) |
||
| Línea 4: | Línea 4: | ||
expresiones carece de sentido en el álgebra vectorial? | expresiones carece de sentido en el álgebra vectorial? | ||
| - | :(1) <math>\frac{\lambda\,\vec{a}\cdot\vec{b}}{|\vec{c}\times\vec{d}\,|}</math> | + | :(1) <math>\frac{\lambda\,\vec{a}\cdot\vec{b}}{|\vec{c}\times\vec{d}\,|}</math><qquad> |
:(2) <math>\frac{\vec{a}\times\vec{b}}{(\vec{c}\cdot\vec{d}\,)}</math> | :(2) <math>\frac{\vec{a}\times\vec{b}}{(\vec{c}\cdot\vec{d}\,)}</math> | ||
Revisión de 12:38 11 mar 2015
1 Enunciado
Si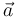 
, 
, 
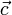y 
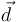son vectores
libres, y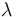 
es un escalar, ¿cuál de las cuatro siguientes
expresiones carece de sentido en el álgebra vectorial?
- (1)
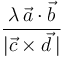<qquad>
- (2)
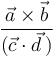
- (3)
![\vec{a}\cdot[\vec{b}\times(\vec{c}\cdot\vec{d}\,)]](/wiki/images/math/c/1/3/c132a4a94ea89ad17bc716c7276bec3b.png)
- (4)
![\vec{a}\times[(\vec{b}\times\vec{c}\,)+\lambda\,\vec{d}\,\,]](/wiki/images/math/5/7/6/576e6b5b251e8d331940a9f5616e8ec0.png)
2 Solución
La expresión (3) es la única que carece de sentido. El producto escalar de 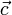y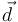 
da como resultado un escalar, y por eso no tiene sentido que 
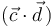aparezca multiplicado vectorialmente por el vector 
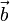(expresión dentro de los corchetes). El producto vectorial es un producto entre dos vectores; no existe el producto vectorial de un vector por un escalar.
