Compresión isoterma de un gas
De Laplace
(→Enunciado) |
|||
| Línea 10: | Línea 10: | ||
Al ser esta presión superior a la interior, aparece una fuerza sobre el pistón y este desciende. Al hacerlo comprime el gas, aumentando su presión. En un proceso real, la presión interior llega a superar a la exterior, causando una fuerza hacia arriba y un “rebote” del émbolo. Tras una serie de oscilaciones, el pistón se detiene en una posición de equilibrio, en la que la presión del gas iguala a la exterior. Puesto que en el estado final la temperatura final iguala a la inicial, podemos aplicar la ley de Boyle | Al ser esta presión superior a la interior, aparece una fuerza sobre el pistón y este desciende. Al hacerlo comprime el gas, aumentando su presión. En un proceso real, la presión interior llega a superar a la exterior, causando una fuerza hacia arriba y un “rebote” del émbolo. Tras una serie de oscilaciones, el pistón se detiene en una posición de equilibrio, en la que la presión del gas iguala a la exterior. Puesto que en el estado final la temperatura final iguala a la inicial, podemos aplicar la ley de Boyle | ||
| - | <center><math> | + | <center><math>p_AV_A = p_BV_B\,</math></center> |
siendo | siendo | ||
| - | <center><math> | + | <center><math>p_A = p_\mathrm{atm}\qquad V_A = Sh_A\qquad\qquad p_B= p_\mathrm{atm}+\frac{mg}{S}\qquad V_B = Sh_B</math></center> |
lo que nos da | lo que nos da | ||
| - | <center><math>p_\mathrm{atm} | + | <center><math>p_\mathrm{atm}h_A = \left(p_\mathrm{atm}+\frac{mg}{S}\right)h_B \qquad\Rightarrow\qquad h_B = \frac{p_\mathrm{atm}}{p_\mathrm{atm}+mg/S}h_A</math></center> |
Sustituyendo los valores numéricos | Sustituyendo los valores numéricos | ||
| - | <center><math> | + | <center><math>h_B = \frac{10^5\,\mathrm{Pa}}{\left(10^5+4.0\cdot 10/(0.04^2)\right)\mathrm{Pa}}10.0\,\mathrm{cm} = 8\,\mathrm{cm}</math></center> |
| - | Vemos que la bajada del pistón es | + | Vemos que la bajada del pistón es pequeña, ya que el incremento de la presión supone solo |
| - | <center><math>\frac{\Delta p}{p_\mathrm{atm}} = \frac{mg}{p_\mathrm{atm}S}= | + | <center><math>\frac{\Delta p}{p_\mathrm{atm}} = \frac{mg}{p_\mathrm{atm}S}=20\%</math></center> |
| - | Esto muestra lo grande que es realmente la presión atmosférica, ya que la fuerza que ejerce equivale la que crearía una pesa de unos | + | y esto considerando un peso muy elevado, ya que para conseguir 4kg de mercurio, por ejemplo, en un tubo de 16cm² de sección hace falta añadir 18cm de mercurio, lo que es muy elevado (la cámara de aire mide solo 10cm). |
| + | |||
| + | Esto muestra lo grande que es realmente la presión atmosférica, ya que la fuerza que ejerce equivale la que crearía una pesa de unos 16 kg, por lo que una de solo 4 kg no hace mucha mella. | ||
==Calentamiento isóbaro== | ==Calentamiento isóbaro== | ||
En el segundo proceso la presión permanece constante, mientras que el volumen aumenta con la temperatura. En este caso la ley de los gases ideales se reduce a la ley de Charles | En el segundo proceso la presión permanece constante, mientras que el volumen aumenta con la temperatura. En este caso la ley de los gases ideales se reduce a la ley de Charles | ||
| - | <center><math>\frac{ | + | <center><math>\frac{V_B}{T_B}=\frac{V_C}{T_C}</math></center> |
donde | donde | ||
| - | <center><math> | + | <center><math>V_B = Sh_B\qquad T_B = T_A\qquad\qquad V_C = V_A = Sh_A</math></center> |
lo que resulta en | lo que resulta en | ||
| - | <center><math> | + | <center><math>T_C = \frac{h_A}{h_B}T_A = \frac{10.0}{8.0}300\,\mathrm{K} = 375\,\mathrm{K} = 102\,^\circ\mathrm{C}</math></center> |
| - | El incremento de temperatura necesario es entonces igual a | + | El incremento de temperatura necesario es entonces igual a 75°C |
[[Categoría:Problemas de introducción a la termodinámica (GIE)]] | [[Categoría:Problemas de introducción a la termodinámica (GIE)]] | ||
Revisión de 18:07 23 feb 2015
1 Enunciado
Un cilindro vertical de sección cuadrada (esto es, un prisma) de 4.0 cm de lado contiene hidrógeno a 27$^\circ$C y 100\,kPa de presión, que también es la temperatura y presión exterior. La tapa del cilindro puede deslizarse sin rozamiento e inicialmente se encuentra a 10.0 cm de altura. Se coloca sobre la tapa una pesa de 4.0 kg. Halle la altura de la tapa una vez que se alcanza de nuevo el equilibrio térmico con el exterior. ¿A qué temperatura habrá que calentar el gas para que la tapa vuelva a su posición inicial, con el peso
todavía encima? (tómese 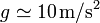 )
)
2 Compresión isoterma
Cuando se coloca la pesa sobre el émbolo, aumenta la presión sobre el gas, siendo la nueva presión ejercida

Al ser esta presión superior a la interior, aparece una fuerza sobre el pistón y este desciende. Al hacerlo comprime el gas, aumentando su presión. En un proceso real, la presión interior llega a superar a la exterior, causando una fuerza hacia arriba y un “rebote” del émbolo. Tras una serie de oscilaciones, el pistón se detiene en una posición de equilibrio, en la que la presión del gas iguala a la exterior. Puesto que en el estado final la temperatura final iguala a la inicial, podemos aplicar la ley de Boyle
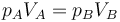
siendo
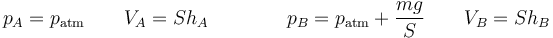
lo que nos da
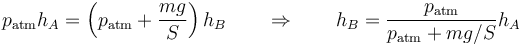
Sustituyendo los valores numéricos
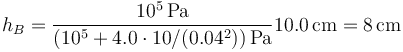
Vemos que la bajada del pistón es pequeña, ya que el incremento de la presión supone solo
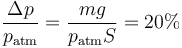
y esto considerando un peso muy elevado, ya que para conseguir 4kg de mercurio, por ejemplo, en un tubo de 16cm² de sección hace falta añadir 18cm de mercurio, lo que es muy elevado (la cámara de aire mide solo 10cm).
Esto muestra lo grande que es realmente la presión atmosférica, ya que la fuerza que ejerce equivale la que crearía una pesa de unos 16 kg, por lo que una de solo 4 kg no hace mucha mella.
3 Calentamiento isóbaro
En el segundo proceso la presión permanece constante, mientras que el volumen aumenta con la temperatura. En este caso la ley de los gases ideales se reduce a la ley de Charles
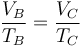
donde

lo que resulta en
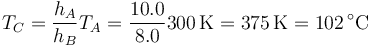
El incremento de temperatura necesario es entonces igual a 75°C





