Vector superficie
De Laplace
(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Nueva página: ==Enunciado== Demuestre que integrando alrededor de una curva cerrada, <math>\Gamma</math>, del plano <math>XY</math>, se cumple que <center><math>\left| \oint_{\Gamma} \mathbf{r} \t...)
Edición más nueva →
(Nueva página: ==Enunciado== Demuestre que integrando alrededor de una curva cerrada, <math>\Gamma</math>, del plano <math>XY</math>, se cumple que <center><math>\left| \oint_{\Gamma} \mathbf{r} \t...)
Edición más nueva →
Revisión de 17:52 24 dic 2008
1 Enunciado
Demuestre que integrando alrededor de una curva cerrada, Γ, del plano XY, se cumple que
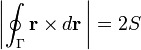
donde 
es el vector de posición y S el área encerrada por Γ.
A partir de aquí, deduzca que para una curva arbitraria en el espacio
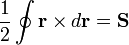
donde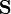 
es un vector cuyas componentes son las áreas de las proyecciones de la curva sobre los planos
coordenados.
