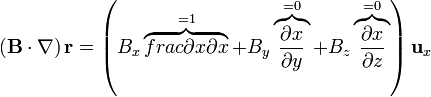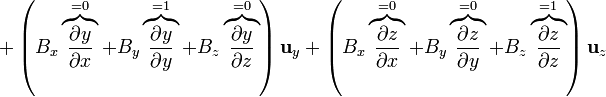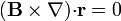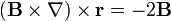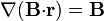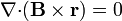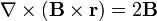Algunas identidades vectoriales
De Laplace
(Diferencias entre revisiones)
(→<math>(\mathbf{B}{\cdot}\nabla)\mathbf{r}=\mathbf{B}</math>) |
(→<math>(\mathbf{B}{\cdot}\nabla)\mathbf{r}=\mathbf{B}</math>) |
||
| Línea 24: | Línea 24: | ||
<center><math>\left(\mathbf{B}\cdot\nabla\right)\mathbf{A}= \left(B_x\frac{\partial A_x}{\partial x}+B_y\frac{\partial A_x}{\partial y}+B_z\frac{\partial A_x}{\partial z}\right)\mathbf{u}_x</math><math>+\left(B_x\frac{\partial A_y}{\partial x}+B_y\frac{\partial A_y}{\partial y}+B_z\frac{\partial A_y}{\partial z}\right)\mathbf{u}_y+ \left(B_x\frac{\partial A_z}{\partial x}+B_y\frac{\partial A_z}{\partial y}+B_z\frac{\partial A_z}{\partial z}\right)\mathbf{u}_z</math></center> | <center><math>\left(\mathbf{B}\cdot\nabla\right)\mathbf{A}= \left(B_x\frac{\partial A_x}{\partial x}+B_y\frac{\partial A_x}{\partial y}+B_z\frac{\partial A_x}{\partial z}\right)\mathbf{u}_x</math><math>+\left(B_x\frac{\partial A_y}{\partial x}+B_y\frac{\partial A_y}{\partial y}+B_z\frac{\partial A_y}{\partial z}\right)\mathbf{u}_y+ \left(B_x\frac{\partial A_z}{\partial x}+B_y\frac{\partial A_z}{\partial y}+B_z\frac{\partial A_z}{\partial z}\right)\mathbf{u}_z</math></center> | ||
| + | Cuando <math>\mathbf{A}=\mathbf{r}</math> esta expresión se simplifica notablemente, ya que | ||
| + | |||
| + | <center><math>\mathbf{r}=x\mathbf{u}_x + y\mathbf{u}_y+z\mathbf{u}_z</math></center> | ||
| + | |||
| + | y queda | ||
| + | |||
| + | <center><math>\left(\mathbf{B}\cdot\nabla\right)\mathbf{r}= \left(B_x\overbrace{frac{\partial x}{\partial x}}^{=1}+B_y\overbrace{\frac{\partial x}{\partial y}}^{=0}+B_z\overbrace{\frac{\partial x}{\partial z}}^{=0}\right)\mathbf{u}_x</math><math>+\left(B_x\overbrace{\frac{\partial y}{\partial x}}^{=0}+B_y\overbrace{\frac{\partial y}{\partial y}}^{=1}+B_z\overbrace{\frac{\partial y}{\partial z}}^{=0}\right)\mathbf{u}_y+ \left(B_x\overbrace{\frac{\partial z}{\partial x}}^{=0}+B_y\overbrace{\frac{\partial z}{\partial y}}^{=0}+B_z\overbrace{\frac{\partial z}{\partial z}}^{=1}\right)\mathbf{u}_z</math></center> | ||
[[Categoría:Problemas de fundamentos matemáticos]] | [[Categoría:Problemas de fundamentos matemáticos]] | ||
Revisión de 11:44 20 dic 2008
1 Enunciado
Demuestre que si  es el vector de posición y
es el vector de posición y  un campo vectorial arbitrario
un campo vectorial arbitrario
Igualmente, para el caso particular en que  represente un vector constante, demuestre que
represente un vector constante, demuestre que
2 Solución
2.1 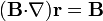
El operador escalar 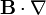 se expresa, en cartesianas, como
se expresa, en cartesianas, como
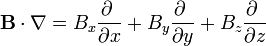
Cuando este operador actúa sobre un campo vectorial, el resultado es la suma de nueve términos, ya que hay que “multiplicar” este operador vectorial por cada una de las componentes del campo vectorial sobre el que actúa:
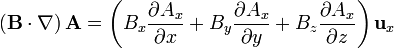
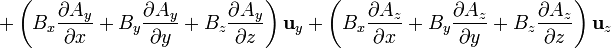
Cuando 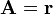 esta expresión se simplifica notablemente, ya que
esta expresión se simplifica notablemente, ya que
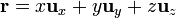
y queda