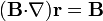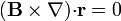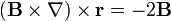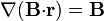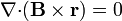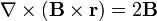Algunas identidades vectoriales
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Enunciado== Demuestre que si <math>\mathbf{r}</math> es el vector de posición y <math>\mathbf{B}</math> un campo vectorial arbitrario # <math>(\mathbf{B}{\cdot}\nabla)\mathbf{r}=\...) |
(→Enunciado) |
||
| Línea 6: | Línea 6: | ||
# <math>(\mathbf{B}\times\nabla)\times\mathbf{r}=-2\mathbf{B}</math> | # <math>(\mathbf{B}\times\nabla)\times\mathbf{r}=-2\mathbf{B}</math> | ||
| - | Igualmente, para el caso particular en que | + | Igualmente, para el caso particular en que <math>\mathbf{B}</math> represente un vector constante, demuestre que |
<ol start="4"> | <ol start="4"> | ||
Revisión de 10:23 20 dic 2008
1 Enunciado
Demuestre que si 
es el vector de posición y 
un campo vectorial arbitrario
Igualmente, para el caso particular en que represente un vector constante, demuestre que
