Entrar Página Discusión Historial Go to the site toolbox

Colisión elástica en el plano

De Laplace

(Diferencias entre revisiones)
 
Línea 52: Línea 52:
<center>[[Archivo:colision-elastica-plano.png]]</center>
<center>[[Archivo:colision-elastica-plano.png]]</center>
-
 
==Velocidades==
==Velocidades==
 +
De acuerdo con esta construcción, el ángulo &theta; que forma la velocidad del proyectil tras la colisión con la que tenía antes de ella, se obtiene por la definición de coseno
 +
 +
<center><math>\cos(\theta)=\frac{|\vec{v}_1|}{|\vec{v}_0|} = \frac{96}{100}=0.96\qquad\Rightarrow\qquad\mathrm{sen}(\theta)=0.28</math></center>
 +
 +
y por tanto el vector velocidad del proyectil tras la colisión equivale a
 +
 +
<center><math>\vec{v}_1=|\vec{v}_1|\left(\cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath}\right)</math></center>
 +
 +
con el valor numérico
 +
 +
<center><math>\vec{v}_1=96(0.96\vec{\imath}+0.28\vec{\jmath})\frac{\mathrm{m}}{\mathrm{s}}=\left(92.16\vec{\imath}+26.88\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
 +
La velocidad del blanco la podemos hallar restando de la velocidad inicial
 +
 +
<center><math>\vec{v}_2=\vec{v}_0-\vec{v}_1=\left(-7.84\vec{\imath}+26.88\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
 +
o bien empleando un método análogo al de la velocidad del proyectil.
 +
 +
==Solución alternativa==
 +
Este problema puede resolverse sin necesidad de construcciones geométricas, resolviendo el sistema de ecuaciones correspondientes
 +
 +
<center><math>\vec{v}_0=\vec{v}_1+\vec{v}_2\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}v_{1x}+v_{2x} & = & 100 \\ v_{1z}+v_{2z} & = & 0\end{array}\right.</math></center>
 +
 +
junto con
 +
 +
<center><math>v_{2x}^2+v_{2z}^2 = 28^2\qquad\qquad (v_{1x}^2+v_{1z}^2)+(v_{2x}^2+v_{2z}^2) = 100^2</math></center>
 +
 +
aunque es más laborioso.
[[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]]
[[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]]

última version al 12:57 7 dic 2014

Contenido

1 Enunciado

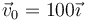Una partícula de masa m = 0.1\,\mathrm{kg} que se mueve con velocidad \vec{v}_0 = 100\vec{\imath} (m/s) colisiona elásticamente con un blanco de la misma masa, que se encuentra en reposo en el origen de coordenadas. Tras la colisión, el blanco se mueve con una rapidez de 28 m/s. Calcule, para el instante posterior a la colisión:

  1. La rapidez del proyectil.
  2. El ángulo que forman las velocidades.
  3. La velocidad de cada partícula.

2 Introducción

En una colisión elástica se conserva tanto la cantidad de movimiento

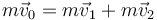
m\vec{v}_0=m\vec{v}_1+m\vec{v}_2

como la energía cinética

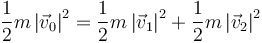
\frac{1}{2}m\left|\vec{v}_0\right|^2=\frac{1}{2}m\left|\vec{v}_1\right|^2+\frac{1}{2}m\left|\vec{v}_2\right|^2

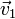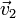donde \vec{v}_1 y \vec{v}_2 son las velocidades del proyectil y del blanco, respectivamente, tras la colisión y hemos usado que la masa de ambos es la misma.

Al ser iguales las masas, podemos simplificar estas dos ecuaciones y escribirlas como

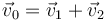
\vec{v}_0=\vec{v}_1+\vec{v}_2

y

\left|\vec{v}_0\right|^2=\left|\vec{v}_1\right|^2+\left|\vec{v}_2\right|^2

3 Rapidez del proyectil

De la segunda de estas dos ecuaciones podemos despejar la rapidez del proyectil

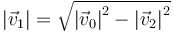
\left|\vec{v}_1\right| = \sqrt{\left|\vec{v}_0\right|^2-\left|\vec{v}_2\right|^2}

que en nuestro caso da

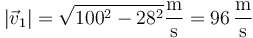
\left|\vec{v}_1\right| = \sqrt{100^2-28^2}\frac{\mathrm{m}}{\mathrm{s}}=96\,\frac{\mathrm{m}}{\mathrm{s}}

4 Ángulo entre las velocidades

Si la ley de conservación de la cantidad de movimiento la multiplicamos escalarmente por sí misma, queda

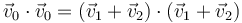
\vec{v}_0\cdot\vec{v}_0=(\vec{v}_1+\vec{v}_2)\cdot(\vec{v}_1+\vec{v}_2)

y desarrollando aquí

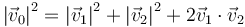
\left|\vec{v}_0\right|^2=\left|\vec{v}_1\right|^2+\left|\vec{v}_2\right|^2+2\vec{v}_1\cdot\vec{v}_2

Comparando este resultado con la ley de conservación de la energía cinética queda

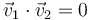
\vec{v}_1\cdot\vec{v}_2=0

Es decir, tras la colisión, las velocidades del proyectil y del blanco son ortogonales.

Una interpretación gráfica de esto es la siguiente: La conservación de la cantidad de movimiento nos dice que la suma de las velocidades finales equivale a la velocidad inicial. La conservación de la energía cinética equivale a un teorema de Pitágoras para los módulos. Por tanto, ambas leyes nos dicen conjuntamente que las velocidades finales son los catetos de un triángulo rectángulo cuya hipotenusa en la velocidad inicial.

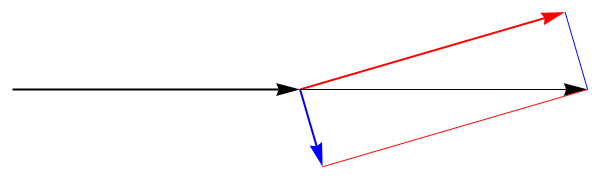
Archivo:colision-elastica-plano.png

5 Velocidades

De acuerdo con esta construcción, el ángulo θ que forma la velocidad del proyectil tras la colisión con la que tenía antes de ella, se obtiene por la definición de coseno

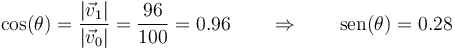
\cos(\theta)=\frac{|\vec{v}_1|}{|\vec{v}_0|} = \frac{96}{100}=0.96\qquad\Rightarrow\qquad\mathrm{sen}(\theta)=0.28

y por tanto el vector velocidad del proyectil tras la colisión equivale a

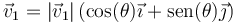
\vec{v}_1=|\vec{v}_1|\left(\cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath}\right)

con el valor numérico

\vec{v}_1=96(0.96\vec{\imath}+0.28\vec{\jmath})\frac{\mathrm{m}}{\mathrm{s}}=\left(92.16\vec{\imath}+26.88\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}}

La velocidad del blanco la podemos hallar restando de la velocidad inicial

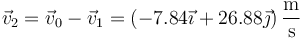
\vec{v}_2=\vec{v}_0-\vec{v}_1=\left(-7.84\vec{\imath}+26.88\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}}

o bien empleando un método análogo al de la velocidad del proyectil.

6 Solución alternativa

Este problema puede resolverse sin necesidad de construcciones geométricas, resolviendo el sistema de ecuaciones correspondientes

\vec{v}_0=\vec{v}_1+\vec{v}_2\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}v_{1x}+v_{2x} & = & 100 \\ v_{1z}+v_{2z} & = & 0\end{array}\right.

junto con

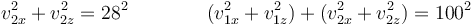
v_{2x}^2+v_{2z}^2 = 28^2\qquad\qquad (v_{1x}^2+v_{1z}^2)+(v_{2x}^2+v_{2z}^2) = 100^2

aunque es más laborioso.

Obtenido de "http://tesla.us.es/wiki/index.php/Colisi%C3%B3n_el%C3%A1stica_en_el_plano"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 12:57, 7 dic 2014. - Esta página ha sido visitada 2.154 veces. - Aviso legal - Acerca de Laplace