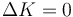Colisión con un obstáculo circular

De Laplace

(Diferencias entre revisiones)

Revisión de 11:11 1 dic 2014

Contenido

1 Enunciado
2 Introducción
3 Velocidad antes y después
4 Cantidad de movimiento
5 Momento cinético
6 Energía cinética

1 Enunciado

Una partícula de masa 1 mg que se mueve uniformemente en el plano XY sobre la recta 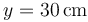$y = 30\,\mathrm{cm}$ con rapidez constante 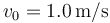$v_0 = 1.0\,\mathrm{m}/\mathrm{s}$ procedente de 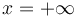$x = +\infty$ colisiona con un obstáculo circular de radio 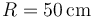$R = 50\,\mathrm{cm}$ centrado en el origen de coordenadas. En la colisión

la componente de la velocidad tangente al obstáculo no cambia.
la componente perpendicular al obstáculo cambia de signo.

Halle la velocidad antes y después de la colisión.
calcule como cambian en la colisión
1. la cantidad de movimiento,
2. el momento cinético respecto al origen y
3. la energía cinética.

2 Introducción

Este problema es la versión más simple del estudio de la dispersión (scattering en inglés), por el cual partículas que colisionan con un obstáculo (que puede ser sólido, como en este caso, pero también puede ser un campo repulsivo, como el eléctrico) y son desviadas de su dirección de movimiento original. La medida del ángulo de desviación permite determinar las propiedades del obstáculo, en particular su tamaño (la llamada sección eficaz).

El estudio de la dispersión es esencial para el análisis de las interacciones entre partículas, en particular los que tienen lugar en el interior de una central nuclear, donde la medida de la sección eficaz de los distintos procesos determina el funcionamiento de ésta.

Como planteamiento general, tenemos un obstáculo, centrado en el origen, y una partícula incidente que se mueve en línea recta a una distancia $b$ (parámetro de impacto) de un eje que pasa por el centro del obstáculo. Tras la colisión se desvía un ángulo $θ$ (ángulo de dispersión) respecto a esta dirección.

3 Velocidad antes y después

La velocidad inicial es horizontal y en el sentido del eje X negativo

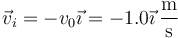
$\vec{v}_i = -v_0\vec{\imath}=-1.0\vec{\imath}\,\frac{\mathrm{m}}{\mathrm{s}}$

La partícula impacta en un punto

$\vec{r}_i=x_i\vec{\imath}+y_i\vec{\jmath}$

formando este vector de posición un cierto ángulo con el eje OX, definido por

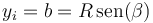
$y_i = b = R\,\mathrm{sen}(\beta)$

y, por tanto,

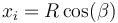
$x_i = R\cos(\beta)\,$

En esta colisión, la componente normal a la superficie de la velocidad cambia de sentido, mientras que la tangencial lo conserva, es decir, que si antes del choque tenemos

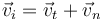
$\vec{v}_i = \vec{v}_t+\vec{v}_n$

tras él la velocidad vale

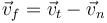
$\vec{v}_f = \vec{v}_t-\vec{v}_n$

Aquí tangente y normal se refieren respecto a la superficie del obstáculo. El vector normal a esta superficie en el punto de impacto es un unitario radial

$\vec{n}=\vec{u}_r=\cos(\beta)\vec{\imath}+\mathrm{sen}(\beta)\vec{\jmath}$

La componente normal de la velocidad la hallamos a partir de la fórmula de la proyección de un vector en una dirección dada

$\vec{v}_n=(\vec{v}\cdot\vec{n})\vec{n}=-v_0\cos(\beta)\left(\cos(\beta)\vec{\imath}+\mathrm{sen}(\beta)\vec{\jmath}\right) = -v_0\cos^2(\beta)\vec{\imath}-v_0\cos(\beta)\mathrm{sen}(\beta)\vec{\jmath}$

La componente tangencial será el resto de la velocidad

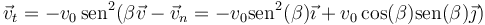
$\vec{v}_t = -v_0\,\mathrm{sen}^2(\beta\vec{v}-\vec{v}_n = -v_0\mathrm{sen}^2(\beta)\vec{\imath}+v_0\cos(\beta)\mathrm{sen}(\beta)\vec{\jmath})$

Por tanto, la velocidad tras el choque vale

$\vec{v}_f = \vec{v}_t-\vec{v}_n = v_0\left(\cos^2(\beta)-\mathrm{sen}^2(\beta)\right)\vec{\imath}+2v_0\cos(\beta)\mathrm{sen}(\beta)\vec{\jmath}=v_0\cos(2\beta)\vec{\imath}+v_0\mathrm{sen}(2\beta)\vec{\jmath}$

Gráficamente, podemos ver que la velocidad se refleja en la superficie, formando a su salida el mismo ángulo con la normal que la velocidad incidente.

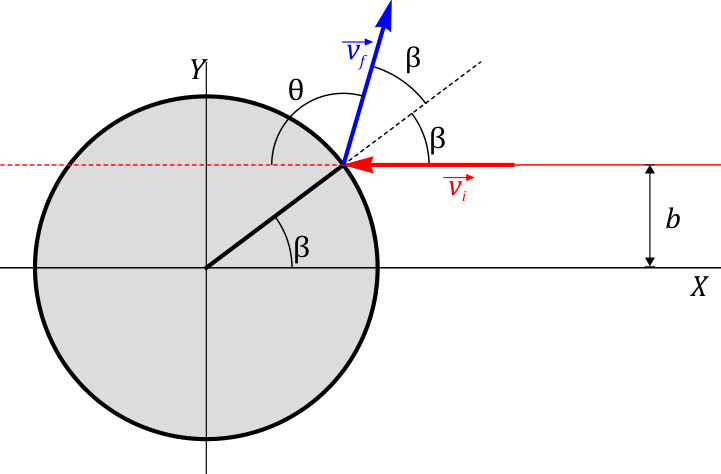
Asimismo, vemos que el ángulo de dispersión será

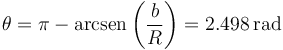
$\theta=\pi-\mathrm{arcsen}\left(\frac{b}{R}\right)=2.498\,\mathrm{rad}$

La rapidez de salida es la misma que la de entrada, $v 0$ .

Aplicando esto a nuestros datos numéricos queda la velocidad inicial

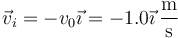
$\vec{v}_i = -v_0\vec{\imath}=-1.0\vec{\imath}\,\frac{\mathrm{m}}{\mathrm{s}}$

El ángulo $β$

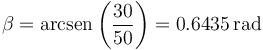
$\beta = \mathrm{arcsen}\left(\frac{30}{50}\right) = 0.6435\,\mathrm{rad}$

El punto de impacto

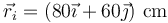
$\vec{r}_i=\left(80\vec{\imath}+60\vec{\jmath}\right)\,\mathrm{cm}$

El vector normal

$\vec{n}=\vec{u}_r=\cos(\beta)\vec{\imath}+\mathrm{sen}(\beta)\vec{\jmath}=0.80\vec{\imath}+0.60\vec{\jmath}$

La componente normal de la velocidad antes del impacto

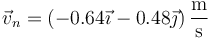
$\vec{v}_n=\left(-0.64\vec{\imath}-0.48\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}}$

y la componente tangencial

$\vec{v}_t=\left(-0.36\vec{\imath}+0.48\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}}$

Por tanto, la velocidad tras la colisión queda

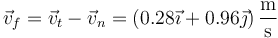
$\vec{v}_f = \vec{v}_t-\vec{v}_n = \left(0.28\vec{\imath}+0.96\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}}$

siendo el ángulo de dispersión

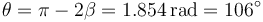
$\theta = \pi-2\beta = 1.854\,\mathrm{rad} = 106^\circ$

4 Cantidad de movimiento

El impulso que recibe la partícula en la colisión es la diferencia entre la cantidad de movimiento posterior y la anterior al choque

$\Delta\vec{p}=m\vec{v}_f-m\vec{v}_i = -2m\vec{v}_n$

Vemos que el impulso tiene una dirección puramente radial y un sentido hacia afuera del círculo. Su valor numérico es

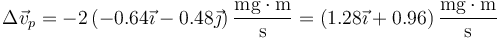
$\Delta\vec{v}_p = -2\left(-0.64\vec{\imath}-0.48\vec{\jmath}\right)\frac{\mathrm{mg}\cdot\mathrm{m}}{\mathrm{s}} = \left(1.28\vec{\imath}+0.96\right)\frac{\mathrm{mg}\cdot\mathrm{m}}{\mathrm{s}}$

5 Momento cinético

El cambio en el momento cinético es igual a

$\Delta\vec{L}_O = m\vec{r}_f\times\vec{v}_f - m\vec{r}_i\times\vec{v}_f$

pero, dado que la posición justo antes del choque y justo después es la misma, podemos extraer el factor común

$\Delta\vec{L}_O = m\vec{r}\times\left(\vec{v}_f-\vec{v}_i\right) = -2m\vec{r}\times\vec{v}_n$

Este es el producto vectorial de dos vectores paralelos (tanto la velocidad normal como la posición son radiales), por lo que el momento cinético se conserva en la colisión

$\Delta\vec{L}_O = \vec{0}$

6 Energía cinética

La energía cinética antes de la colisión es igual a

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): K_i= \frac{1}{2}m\left|\vec{v}_i\right|^2=\frac{1}{2}m\left(|\vec{v}_n}|^2+|\vec{v}_f|^2\right)

y después de ella

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): K_i= \frac{1}{2}m\left|\vec{v}_f\right|^2=\frac{1}{2}m\left(|-\vec{v}_n}|^2+|\vec{v}_f|^2\right)=\frac{1}{2}m\left(|\vec{v}_n}|^2+|\vec{v}_f|^2\right)

En la colisión cambia la dirección de la velocidad, pero no la rapidez. Por ello, se conserva la energía cinética

$\Delta K = 0\,$

@@ Línea 76: / Línea 76: @@
 <center><math>\vec{r}_i=\left(80\vec{\imath}+60\vec{\jmath}\right)\,\mathrm{cm}</math></center>
+El vector normal
+<center><math>\vec{n}=\vec{u}_r=\cos(\beta)\vec{\imath}+\mathrm{sen}(\beta)\vec{\jmath}=0.80\vec{\imath}+0.60\vec{\jmath}</math></center>
 La componente normal de la velocidad antes del impacto
@@ Línea 100: / Línea 104: @@
 <center><math>\Delta\vec{v}_p = -2\left(-0.64\vec{\imath}-0.48\vec{\jmath}\right)\frac{\mathrm{mg}\cdot\mathrm{m}}{\mathrm{s}} = \left(1.28\vec{\imath}+0.96\right)\frac{\mathrm{mg}\cdot\mathrm{m}}{\mathrm{s}}</math></center>
-<center><math>\vec{n}=\vec{u}_r=\cos(\beta)\vec{\imath}+\mathrm{sen}(\beta)\vec{\jmath}=0.80\vec{\imath}+0.60\vec{\jmath}</math></center>
 ==Momento cinético==

Colisión con un obstáculo circular

De Laplace

Revisión de 11:11 1 dic 2014

Contenido

1 Enunciado

2 Introducción

3 Velocidad antes y después

4 Cantidad de movimiento

5 Momento cinético

6 Energía cinética

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES