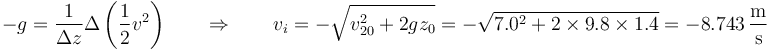Entrar Página Discusión Historial Go to the site toolbox

Piedra y pájaro que se mueven verticalmente

De Laplace

(Diferencias entre revisiones)
Línea 9: Línea 9:
==Máximo valor de ''v''<sub>1</sub>==
==Máximo valor de ''v''<sub>1</sub>==
 +
Para que la piedra alcance al pájaro, debe coincidir en la misma posición en el mismo instante.
 +
 +
La posición instantánea del pájaro es, empleando siempre el SI,
 +
 +
<center><math>z_1 = h_1 + v_1 t = 3.0 + v_1 t\,</math></center>
 +
 +
y la de la piedra
 +
 +
<center><math>z_2 = h_2 + v_2t - \frac{1}{2}gt^2 = 1.4+7.0t-4.9t^2</math></center>
 +
 +
Igualando ambas posiciones queda una ecuación de segundo grado
 +
 +
<center><math>3.0 + v_1 t = 1.4+7.0t-4.9t^2 \qquad\Rightarrow\qquad 4.9t^2 +(v_1-7.0)t+1.6=0</math></center>
 +
 +
con soluciones
 +
 +
<center><math>t = \frac{(7.0-v_1) \pm\sqrt{(7.0-v_1)^2 - 4\times 1.6\times 4.9}}{2\times 4.9}</math></center>
 +
 +
Esta solución no siempre es real, ya que lo que hay dentro de la raíz puede hacerse negativo. Cuando esto ocurre quiere decir que no hay solución y la piedra no alcanza al pájaro.
 +
 +
El máximo valor posible de <math>v_1</math> será entonces el que anule esta cantidad
 +
 +
<center><math>(7.0-v_1)^2 - 31.36 = 0\qquad\Rightarrow\qquad 7.0-v_1 = 5.6 \qquad\Rightarrow\qquad v_1 = 1.4\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
 +
Para esta velocidad, el tiempo que tarda en impactar es
 +
 +
<center><math>t = \frac{5.6}{4.9}\mathrm{s} = \frac{4}{7}\mathrm{s} = 0.571\,\mathrm{s}</math></center>
 +
==Velocidades medias==
==Velocidades medias==
 +
===Del pájaro===
 +
Puesto que se mueve a velocidad constante, la velocidad media coincide con la instantánea
 +
 +
<center><math>v_{m1} = v_1 = 1.4\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
 +
===De la piedra===
 +
Podemos calcular esta velocidad media de varias formas. La más directa es desplazamiento dividido por intervalo. El punto de impacto se produce en
 +
 +
<center><math>z_2 = 1.4 + 7.0\frac{4}{7}-4.9\left(\frac{4}{7}\right)^2 = 3.8\,\mathrm{m}</math></center>
 +
 +
lo que da una velocidad media
 +
 +
<center><math>v_{m2}=\frac{\Delta z_2}{\Delta t} = \frac{3.8-1.4}{4/7} = 4.2\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
==Movimiento de la piedra==
==Movimiento de la piedra==
 +
Para este apartado no hacen falta los dos anteriores. La ecuación horaria de la piedra es
 +
 +
<center><math>z = 1.4+7.0 t - 4.9t^2\,</math></center>
 +
 +
que alcanza el máximo cuando la velocidad se anula
 +
 +
<center><math>0 = v_z = \dot{z}= 7.0-9.8 t\qquad\Rightarrow\qquad t = \frac{5}{7}\,\mathrm{s} = 0.714\,\mathrm{s}</math></center>
 +
 +
y en ese instante su altura es
 +
 +
<center><math>z_{2\mathrm{max}} = 1.4 + 7.0\frac{5}{7}-4.9\left(\frac{5}{7}\right)^2 = 3.9\,\mathrm{m}</math></center>
 +
 +
Alternativamente, esto se puede resolver observando que
 +
 +
<center><math>-g =\frac{1}{\Delta z}\Delta\left(\frac{1}{2}v^2\right)\qquad\Rightarrow\qquad z = z_0+\frac{v_{20}^2}{2g}</math></center>
 +
 +
La partícula impacta en el suelo cuando <math>z=0</math>. Esto ocurre en el instante
 +
 +
<center><math>0 = 1.4+7.0 t - 4.9t^2\qquad\Rightarrow\qquad t = \frac{5 + \sqrt{39}}{7} = 1.606\,\mathrm{s}</math></center>
 +
 +
y la velocidad en ese momento es
 +
 +
<center><math>v_{2i} = 7(5-\sqrt{39})\,\frac{\mathrm{m}}{\mathrm{s}} = -8.743\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
 +
Alternativamente, puede resolverse sin emplear el tiempo, haciendo uso de la relación
 +
 +
<center><math>-g =\frac{1}{\Delta z}\Delta\left(\frac{1}{2}v^2\right)\qquad\Rightarrow\qquad v_i = -\sqrt{v_{20}^2+2gz_0}=-\sqrt{7.0^2+2\times 9.8\times 1.4}=-8.743\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
[[Categoría:Problemas de examen de Física I (GIE)]]
[[Categoría:Problemas de examen de Física I (GIE)]]
[[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]]
[[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]]

Revisión de 17:39 11 nov 2014

Contenido

1 Enunciado

Desde un punto a una altura 1.4 m respecto al suelo, un niño lanza verticalmente una piedra contra un pájaro que está 1.6 m más arriba. La velocidad inicial de la piedra es de 7.0 m/s. Tal como lanza la piedra, el pájaro sale volando hacia arriba con velocidad constante v1.

Despreciando el rozamiento del aire sobre la piedra y tomando g = 9.8 m/s²:

  1. Calcule el máximo valor de v1 con que asciende el pájaro, si la piedra es capaz de alcanzarle.
  2. Suponiendo que ha volado con esta velocidad máxima, calcule la velocidad instantánea de la piedra y del pájaro en el momento del impacto, así como la velocidad media de cada uno desde el lanzamiento hasta ese momento.
  3. Si en lugar de darle la piedra falla por poco y continúa su vuelo, ¿hasta que altura respecto al suelo llega? ¿Qué velocidad tiene cuando impacta de nuevo con el suelo?

2 Máximo valor de v1

Para que la piedra alcance al pájaro, debe coincidir en la misma posición en el mismo instante.

La posición instantánea del pájaro es, empleando siempre el SI,

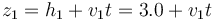
z_1 = h_1 + v_1 t = 3.0 + v_1 t\,

y la de la piedra

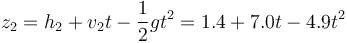
z_2 = h_2 + v_2t - \frac{1}{2}gt^2 = 1.4+7.0t-4.9t^2

Igualando ambas posiciones queda una ecuación de segundo grado

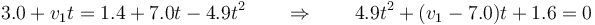
3.0 + v_1 t = 1.4+7.0t-4.9t^2 \qquad\Rightarrow\qquad 4.9t^2 +(v_1-7.0)t+1.6=0

con soluciones

t = \frac{(7.0-v_1) \pm\sqrt{(7.0-v_1)^2 - 4\times 1.6\times 4.9}}{2\times 4.9}

Esta solución no siempre es real, ya que lo que hay dentro de la raíz puede hacerse negativo. Cuando esto ocurre quiere decir que no hay solución y la piedra no alcanza al pájaro.

El máximo valor posible de v1 será entonces el que anule esta cantidad

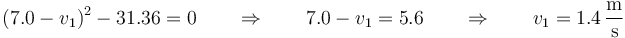
(7.0-v_1)^2 - 31.36 = 0\qquad\Rightarrow\qquad 7.0-v_1 = 5.6 \qquad\Rightarrow\qquad v_1 = 1.4\,\frac{\mathrm{m}}{\mathrm{s}}

Para esta velocidad, el tiempo que tarda en impactar es

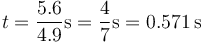
t = \frac{5.6}{4.9}\mathrm{s} = \frac{4}{7}\mathrm{s} = 0.571\,\mathrm{s}

3 Velocidades medias

3.1 Del pájaro

Puesto que se mueve a velocidad constante, la velocidad media coincide con la instantánea

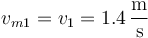
v_{m1} = v_1 = 1.4\,\frac{\mathrm{m}}{\mathrm{s}}

3.2 De la piedra

Podemos calcular esta velocidad media de varias formas. La más directa es desplazamiento dividido por intervalo. El punto de impacto se produce en

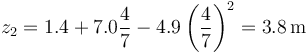
z_2 = 1.4 + 7.0\frac{4}{7}-4.9\left(\frac{4}{7}\right)^2 = 3.8\,\mathrm{m}

lo que da una velocidad media

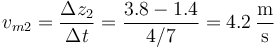
v_{m2}=\frac{\Delta z_2}{\Delta t} = \frac{3.8-1.4}{4/7} = 4.2\,\frac{\mathrm{m}}{\mathrm{s}}

4 Movimiento de la piedra

Para este apartado no hacen falta los dos anteriores. La ecuación horaria de la piedra es

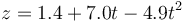
z = 1.4+7.0 t - 4.9t^2\,

que alcanza el máximo cuando la velocidad se anula

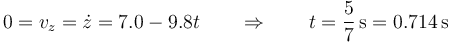
0 = v_z = \dot{z}= 7.0-9.8 t\qquad\Rightarrow\qquad t = \frac{5}{7}\,\mathrm{s} = 0.714\,\mathrm{s}

y en ese instante su altura es

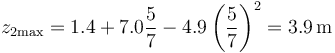
z_{2\mathrm{max}} = 1.4 + 7.0\frac{5}{7}-4.9\left(\frac{5}{7}\right)^2 = 3.9\,\mathrm{m}

Alternativamente, esto se puede resolver observando que

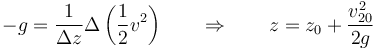
-g =\frac{1}{\Delta z}\Delta\left(\frac{1}{2}v^2\right)\qquad\Rightarrow\qquad z = z_0+\frac{v_{20}^2}{2g}

La partícula impacta en el suelo cuando z = 0. Esto ocurre en el instante

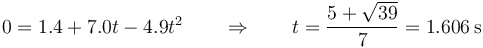
0 = 1.4+7.0 t - 4.9t^2\qquad\Rightarrow\qquad t = \frac{5 + \sqrt{39}}{7} = 1.606\,\mathrm{s}

y la velocidad en ese momento es

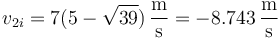
v_{2i} = 7(5-\sqrt{39})\,\frac{\mathrm{m}}{\mathrm{s}} = -8.743\,\frac{\mathrm{m}}{\mathrm{s}}

Alternativamente, puede resolverse sin emplear el tiempo, haciendo uso de la relación

-g =\frac{1}{\Delta z}\Delta\left(\frac{1}{2}v^2\right)\qquad\Rightarrow\qquad v_i = -\sqrt{v_{20}^2+2gz_0}=-\sqrt{7.0^2+2\times 9.8\times 1.4}=-8.743\,\frac{\mathrm{m}}{\mathrm{s}}
Obtenido de "http://tesla.us.es/wiki/index.php/Piedra_y_p%C3%A1jaro_que_se_mueven_verticalmente"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace