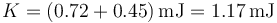Entrar Página Discusión Historial Go to the site toolbox

Rodadura y pivotamiento de una esfera

De Laplace

(Diferencias entre revisiones)
Línea 67: Línea 67:
siendo el momento de inercia
siendo el momento de inercia
-
<center><math>I=\frac{2}{5}MR^2=\frac{2.5}(0.400)(2.5)^2\,\mathrm{kg}\cdot\mathrm{cm}^2=1\,\mathrm{kg}\cdot\mathrm{cm}^2</math></center>
+
<center><math>I=\frac{2}{5}MR^2=\frac{2}{5}(0.400)(2.5)^2\,\mathrm{kg}\cdot\mathrm{cm}^2=1\,\mathrm{kg}\cdot\mathrm{cm}^2</math></center>
Esto da, para el primer término
Esto da, para el primer término

Revisión de 11:57 14 sep 2014

Contenido

1 Enunciado

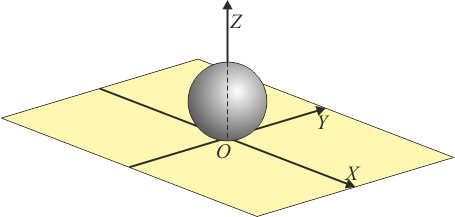
Una esfera maciza de 2.5 cm de radio y 0.400 kg de masa rueda y pivota sin deslizar sobre una superficie horizontal. En un instante dado la velocidad angular de pivotamiento es de 1.80 rad/s en sentido antihorario respecto al eje OZ (tomando como origen el punto de contacto y como eje OZ el perpendicular al plano), mientras que la de rodadura es de 2.40 rad/s en la dirección del vector unitario

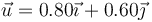
\vec{u}=0.80\vec{\imath}+0.60\vec{\jmath}

Para este instante, calcule:

  1. El vector velocidad angular y la ecuación del eje instantáneo de rotación.
  2. La velocidad y la rapidez del centro de la esfera.
  3. La distancia del centro de la esfera al eje instantáneo de rotación.
  4. La cantidad de movimiento, el momento cinético y la energía cinética de la esfera.

Dato: Momento de inercia de una esfera respecto a un eje que pasa por su centro I = (2 / 5)MR2.

Archivo:bola-sobre-plano.png

2 Velocidad angular y eje

2.1 Velocidad angular

La velocidad angular de pivotamiento corresponde a un giro alrededor del eje OZ. Por ser en sentido antihorario, su sentido es el de 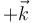+\vec{k}

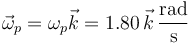
\vec{\omega}_p=\omega_p\vec{k}=1.80\,\vec{k}\,\frac{\mathrm{rad}}{\mathrm{s}}

La de rodadura es en la dirección y sentido que se nos indica

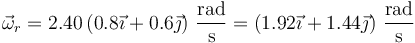
\vec{\omega}_r=2.40\left(0.8\vec{\imath}+0.6\vec{\jmath}\right)\,\frac{\mathrm{rad}}{\mathrm{s}}=\left(1.92\vec{\imath}+1.44\vec{\jmath}\right)\,\frac{\mathrm{rad}}{\mathrm{s}}

La velocidad angular del sólido es la suma de las dos

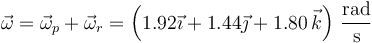
\vec{\omega}=\vec{\omega}_p+\vec{\omega}_r=\left(1.92\vec{\imath}+1.44\vec{\jmath}+1.80\,\vec{k}\right)\,\frac{\mathrm{rad}}{\mathrm{s}}

siendo su módulo

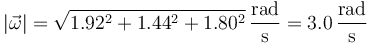
|\vec{\omega}|=\sqrt{1.92^2+1.44^2+1.80^2}\,\frac{\mathrm{rad}}{\mathrm{s}}=3.0\,\frac{\mathrm{rad}}{\mathrm{s}}

2.2 Eje instantáneo de rotación

El EIR es la recta formada por los puntos que tienen velocidad nula. Tiene la dirección de la velocidad angular.

Para hallar un punto por el que pase buscamos uno de velocidad nula. Puesto que se nos dice que rueda y pivota sin deslizar, el propio punto de contacto O es un punto del eje. Por tanto la ecuación de éste es simplemente

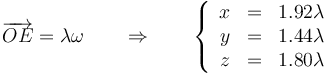
\overrightarrow{OE}=\lambda\omega\qquad\Rightarrow\qquad \left\{\begin{array}{rcl} x & = & 1.92\lambda \\ y & = & 1.44\lambda \\ z & = & 1.80\lambda\end{array}\right.

3 Velocidad y rapidez del CM

La velocidad del centro de la esfera la hallamos por el campo de velocidades de un sólido

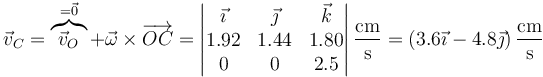
\vec{v}_C=\overbrace{\vec{v}_O}^{=\vec{0}}+\vec{\omega}\times\overrightarrow{OC}=\left|\begin{matrix} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 1.92 & 1.44 & 1.80 \\ 0 & 0 & 2.5\end{matrix}\right|\frac{\mathrm{cm}}{\mathrm{s}}=\left(3.6\vec{\imath}-4.8\vec{\jmath}\right)\frac{\mathrm{cm}}{\mathrm{s}}

siendo la rapidez el módulo de esta velocidad

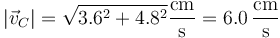
|\vec{v}_C|=\sqrt{3.6^2+4.8^2}\frac{\mathrm{cm}}{\mathrm{s}}=6.0\,\frac{\mathrm{cm}}{\mathrm{s}}

4 Distancia al eje

En un movimiento de rotación la velocidad de un punto es proporcional a la distancia al eje

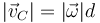
|\vec{v}_C|=|\vec{\omega}|d

Por tanto,

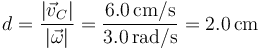
d=\frac{|\vec{v}_C|}{|\vec{\omega}|}=\frac{6.0\,\mathrm{cm}/\mathrm{s}}{3.0\,\mathrm{rad}/\mathrm{s}}=2.0\,\mathrm{cm}

5 Cantidad de movimiento, Momento cinético y energía cinética

5.1 Cantidad de movimiento

La cantidad de movimiento de un sistema de partículas es la misma que tendría una partícula que se moviera como el centro de masas

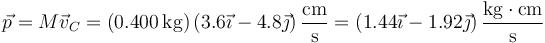
\vec{p}=M\vec{v}_C=\left(0.400\,\mathrm{kg}\right)\left(3.6\vec{\imath}-4.8\vec{\jmath}\right)\frac{\mathrm{cm}}{\mathrm{s}}=\left(1.44\vec{\imath}-1.92\vec{\jmath}\right)\frac{\mathrm{kg}\cdot\mathrm{cm}}{\mathrm{s}}

5.2 Momento cinético

El momento cinético de un sistema es suma del que tendría si se moviera como el centro de masas más el que tiene por moverse alrededor del CM. Para el caso de un sólido, esto es

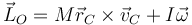
\vec{L}_O=M\vec{r}_C\times\vec{v}_C+I\vec{\omega}

siendo el momento de inercia

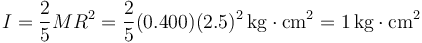
I=\frac{2}{5}MR^2=\frac{2}{5}(0.400)(2.5)^2\,\mathrm{kg}\cdot\mathrm{cm}^2=1\,\mathrm{kg}\cdot\mathrm{cm}^2

Esto da, para el primer término

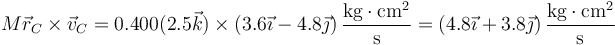
M\vec{r}_C\times\vec{v}_C=0.400(2.5\vec{k})\times\left(3.6\vec{\imath}-4.8\vec{\jmath}\right)\frac{\mathrm{kg}\cdot\mathrm{cm}^2}{\mathrm{s}}=\left(4.8\vec{\imath}+3.8\vec{\jmath}\right)\frac{\mathrm{kg}\cdot\mathrm{cm}^2}{\mathrm{s}}

y para el segundo

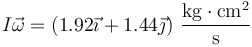
I\vec{\omega}=\left(1.92\vec{\imath}+1.44\vec{\jmath}\right)\,\frac{\mathrm{kg}\cdot\mathrm{cm}^2}{\mathrm{s}}

Sumando las dos contribuciones queda

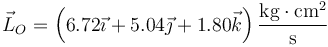
\vec{L}_O=\left(6.72\vec{\imath}+5.04\vec{\jmath}+ 1.80\vec{k}\right)\frac{\mathrm{kg}\cdot\mathrm{cm}^2}{\mathrm{s}}

5.3 Energía cinética

La energía cinética se descompone de manera análoga al momento cinético

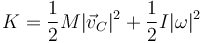
K = \frac{1}{2}M|\vec{v}_C|^2+\frac{1}{2}I|\omega|^2

lo que nos da, para el primer término

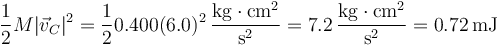
\frac{1}{2}M|\vec{v}_C|^2=\frac{1}{2}0.400(6.0)^2\,\frac{\mathrm{kg}\cdot\mathrm{cm}^2}{\mathrm{s}^2}=7.2\,\frac{\mathrm{kg}\cdot\mathrm{cm}^2}{\mathrm{s}^2}=0.72\,\mathrm{mJ}

y para el segundo

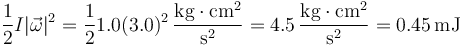
\frac{1}{2}I|\vec{\omega}|^2=\frac{1}{2}1.0(3.0)^2\,\frac{\mathrm{kg}\cdot\mathrm{cm}^2}{\mathrm{s}^2}=4.5\,\frac{\mathrm{kg}\cdot\mathrm{cm}^2}{\mathrm{s}^2}=0.45\,\mathrm{mJ}

siendo el total

K = (0.72+0.45)\,\mathrm{mJ}=1.17\,\mathrm{mJ}
Obtenido de "http://tesla.us.es/wiki/index.php/Rodadura_y_pivotamiento_de_una_esfera"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace