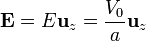Condensador plano
De Laplace
(→Campo eléctrico) |
(→Campo eléctrico) |
||
| Línea 63: | Línea 63: | ||
esto es, el campo eléctrico es independiente de la posición en el espacio entre las placas. | esto es, el campo eléctrico es independiente de la posición en el espacio entre las placas. | ||
| + | |||
| + | Su valor lo sacamos de que conocemos la diferencia de potencial entre las placas. Si consideramos un camino rectilíneo que vaya de una placa a la otra. | ||
| + | |||
| + | <center><math>V_0 = \phi(z=0) -\phi(z=a) = \int_A^B \mathbf{E}\cdot\mathrm{d}\mathbf{r}=\int_0^a E\,\mathrm{d}z = Ea</math></center> | ||
| + | |||
| + | La integral es inmediata por ser el campo uniforme. Despejando | ||
| + | |||
| + | <center><math>\mathbf{E}=E\mathbf{u}_z = \frac{V_0}{a}\mathbf{u}_z</math></center> | ||
===Carga en una de las placas=== | ===Carga en una de las placas=== | ||
Revisión de 11:54 16 dic 2008
Contenido |
1 Enunciado
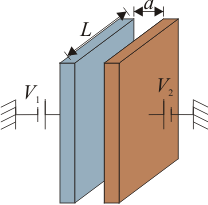
Dos placas conductoras cuadradas de lado L se sitúan paralelamente a una distancia a la una de la otra ( ). Los potenciales de ambas placas son V1 y V2, respectivamente. Calcule el valor aproximado de
). Los potenciales de ambas placas son V1 y V2, respectivamente. Calcule el valor aproximado de
- El potencial en los puntos entre ambas placas.
- El campo eléctrico en el espacio intermedio.
- La carga almacenada en la caras de las placas enfrentadas a la otra placa.
Desprecie los efectos de borde.
2 Solución
2.1 Potencial eléctrico
Como en el caso del condensador coaxial si consideramos el caso de dos placas de área finita, el problema completo precisa incluir la zona exterior a las placas. Esto requiere el uso de métodos numéricos o avanzadas técnicas analíticas (como el empleo de variable compleja y transformaciones conformes).
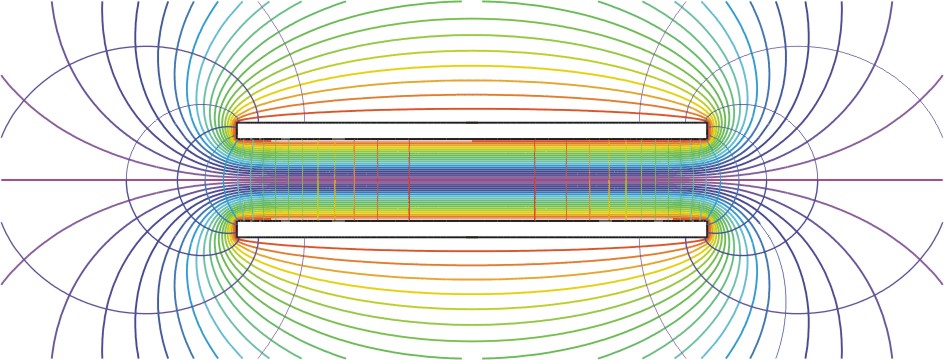
Sin embargo, si la distancia entre placas es mucho menos que las dimensiones laterales de estas, podemos hacer la aproximación de que el campo se concentra sólo en el espacio entre ellas. y que además va en la dirección perpendicular a las placas (dirección que tomamos como eje Z). Según esto

Igualando esto al gradiente del potencial cambiado de signo, expresado en cartesianas o en cilíndricas, resulta
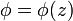
y si el potencial depende exclusivamente de la coordenada ortogonal a las placas, la ecuación de Laplace se reduce a
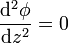
con las condiciones de contorno
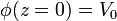
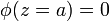
La solución de la ecuación diferencial es, simplemente,
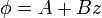
y, tras aplicar las condiciones de contorno
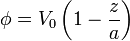
2.2 Campo eléctrico
Conocido el potencial, el campo es inmediato.
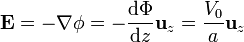
Resulta un campo uniforme en todo el espacio entre las placas.
Este campo puede también determinarse sin pasar por el potencial eléctrico. Si partimos de las leyes de la electrostática


y suponemos que el campo va en la dirección perpendicular a las placas

estas leyes nos dan
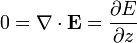
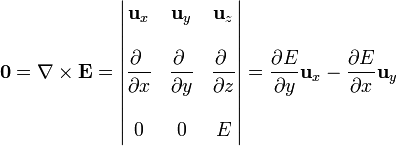
y, por tanto,
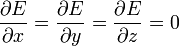
esto es, el campo eléctrico es independiente de la posición en el espacio entre las placas.
Su valor lo sacamos de que conocemos la diferencia de potencial entre las placas. Si consideramos un camino rectilíneo que vaya de una placa a la otra.
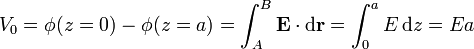
La integral es inmediata por ser el campo uniforme. Despejando