Máquina eléctrica lineal
De Laplace
(→Enunciado) |
|||
| Línea 23: | Línea 23: | ||
Por tanto, la corriente que circula por el circuito es | Por tanto, la corriente que circula por el circuito es | ||
| - | <center><math>I = \frac{\mathcal{E}_0-B_0bv}{ | + | <center><math>I = \frac{\mathcal{E}_0-B_0bv}{r}</math></center> |
El campo magnético produce fuerza sobre esta corriente de acuerdo con la ley de Lorentz | El campo magnético produce fuerza sobre esta corriente de acuerdo con la ley de Lorentz | ||
| - | <center><math>\vec{F}=I( | + | <center><math>\vec{F}=I(b\vec{\jmath})\times(B_0\vec{k})=IbB_0\vec{\imath}</math></center> |
Si aquí sustituimos el valor de la corriente queda | Si aquí sustituimos el valor de la corriente queda | ||
| - | <center><math>\vec{F}=\frac{(\mathcal{E}_0- | + | <center><math>\vec{F}=\frac{(\mathcal{E}_0-B_0bv)bB_0}{r}\vec{\imath}</math></center> |
Esta fuerza se anula si | Esta fuerza se anula si | ||
| - | <center><math>v=v_0=\frac{\mathcal{E}_0}{ | + | <center><math>v=v_0=\frac{\mathcal{E}_0}{bB_0}</math></center> |
Para este valor de la velocidad, la fuerza electromotriz inducida se cancela con la de la fuente, por lo que la corriente que fluye por el circuito es nula y también lo es la fuerza sobre la barra. | Para este valor de la velocidad, la fuerza electromotriz inducida se cancela con la de la fuente, por lo que la corriente que fluye por el circuito es nula y también lo es la fuerza sobre la barra. | ||
| Línea 42: | Línea 42: | ||
Si la velocidad <math>v</math> es menor que <math>v_0</math>, se cumple que | Si la velocidad <math>v</math> es menor que <math>v_0</math>, se cumple que | ||
| - | <center><math>\mathcal{E}_0- | + | <center><math>\mathcal{E}_0-B_0bv =B_0b(v_0-v) > 0</math></center> |
Esto implica que la fuerza sobre la barra va en el sentido de <math>+\vec{\imath}</math> y por tanto tiende a aumentar la velocidad. | Esto implica que la fuerza sobre la barra va en el sentido de <math>+\vec{\imath}</math> y por tanto tiende a aumentar la velocidad. | ||
| Línea 48: | Línea 48: | ||
A la inversa ocurre si <math>v > v_0</math> | A la inversa ocurre si <math>v > v_0</math> | ||
| - | <center><math>\mathcal{E}_0- | + | <center><math>\mathcal{E}_0-B_0bv =B_0b(v_0-v) < 0</math></center> |
En ese caso, la fuerza va en el sentido de <math>-\vec{\imath}</math> y tiende a frenar la barra. | En ese caso, la fuerza va en el sentido de <math>-\vec{\imath}</math> y tiende a frenar la barra. | ||
| Línea 62: | Línea 62: | ||
La velocidad, la aceleración y la fuerza van todas en la misma dirección, por lo que podemos usar cantidades escalares y escribirla como | La velocidad, la aceleración y la fuerza van todas en la misma dirección, por lo que podemos usar cantidades escalares y escribirla como | ||
| - | <center><math>m\frac{\mathrm{d}v}{\mathrm{d}t}=\frac{(\mathcal{E}_0- | + | <center><math>m\frac{\mathrm{d}v}{\mathrm{d}t}=\frac{(\mathcal{E}_0-B_0bv)bB_0}{r}\qquad\qquad v(t=0) = 0</math></center> |
Para resolverla, sacamos factor común de algunos términos | Para resolverla, sacamos factor común de algunos términos | ||
| - | <center><math>\frac{\mathrm{d}v}{\mathrm{d}t}=\frac{( | + | <center><math>\frac{\mathrm{d}v}{\mathrm{d}t}=\frac{(B_0b)^2}{mr}(v_0-v)</math></center> |
Dado que si la velocidad es menor que <math>v_0</math>, la fuerza acelera a la barra, pero si es mayor la frena, concluimos que la barra tiende a moverse con velocidad <math>v_0</math>. Por ello, podemos escribir la velocidad en cualquier instante como | Dado que si la velocidad es menor que <math>v_0</math>, la fuerza acelera a la barra, pero si es mayor la frena, concluimos que la barra tiende a moverse con velocidad <math>v_0</math>. Por ello, podemos escribir la velocidad en cualquier instante como | ||
| Línea 74: | Línea 74: | ||
En términos de esta variable u, la ecuación diferencial queda | En términos de esta variable u, la ecuación diferencial queda | ||
| - | <center><math>\frac{\mathrm{d}u}{\mathrm{d}t}=-\frac{( | + | <center><math>\frac{\mathrm{d}u}{\mathrm{d}t}=-\frac{(B_0b)^2}{mr}u</math></center> |
cuya solución es | cuya solución es | ||
| - | <center><math>u = -v_0\mathrm{e}^{-t/\tau}\qquad\qquad \tau = \frac{ | + | <center><math>u = -v_0\mathrm{e}^{-t/\tau}\qquad\qquad \tau = \frac{mr}{(B_0b)^2}</math></center> |
La solución de la ecuación completa es entonces | La solución de la ecuación completa es entonces | ||
Revisión de 21:06 13 jun 2014
Contenido |
1 Enunciado
Un modelo sencillo de máquina eléctrica sería el siguiente. Se tiene un campo magnético uniforme 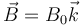 . En el interior de este campo se halla un circuito formado por una fuente de corriente continua, de fuerza electromotriz
. En el interior de este campo se halla un circuito formado por una fuente de corriente continua, de fuerza electromotriz 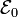 y resistencia r, dos raíles perfectamente conductores, situados paralelamente a una distancia b, y una barra de masa m, también perfectamente conductora, que desliza sin rozamiento por los raíles
(ver figura).
y resistencia r, dos raíles perfectamente conductores, situados paralelamente a una distancia b, y una barra de masa m, también perfectamente conductora, que desliza sin rozamiento por los raíles
(ver figura).
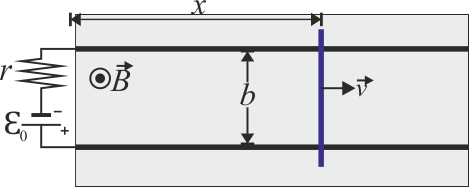
- Suponga que en un instante dado la barra se mueve con velocidad v alejándose de la fuente. ¿Qué intensidad de corriente circula por ella? ¿Qué fuerza se ejerce sobre ella? ¿Para qué valor de la velocidad, v0, esta intensidad de corriente es nula?
- Demuestre que si la velocidad de la barra es v < v0, la barra tiende a acelerarse, mientras que si es mayor tiende a frenarse, por lo que la barra tiende a moverse con velocidad constante.
- Suponga que inicialmente el circuito está abierto, la barra en reposo, y en t = 0 se cierra el interruptor. Aplicando los resultados del primer apartado, determine la ecuación de movimiento para la barra. Resuelva esta ecuación mostrando que la barra sale disparada con una velocidad que tiende a ser constante. Este sería un cañón electromagnético railgun.
2 Velocidad constante
La corriente que circula por el circuito es igual a
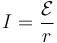
siendo la fuerza electromotriz la suma de las presentes en el circuito. Estas son la debida a la fuente de tensión y la asociada al cambio del flujo magnético
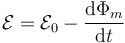
A su vez, este último término viene dado por

Por tanto, la corriente que circula por el circuito es

El campo magnético produce fuerza sobre esta corriente de acuerdo con la ley de Lorentz
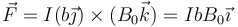
Si aquí sustituimos el valor de la corriente queda

Esta fuerza se anula si
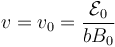
Para este valor de la velocidad, la fuerza electromotriz inducida se cancela con la de la fuente, por lo que la corriente que fluye por el circuito es nula y también lo es la fuerza sobre la barra.
3 Fuerzas
Si la velocidad v es menor que v0, se cumple que
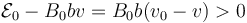
Esto implica que la fuerza sobre la barra va en el sentido de 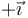 y por tanto tiende a aumentar la velocidad.
y por tanto tiende a aumentar la velocidad.
A la inversa ocurre si v > v0

En ese caso, la fuerza va en el sentido de 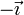 y tiende a frenar la barra.
y tiende a frenar la barra.
Desde el punto de vista energético, en el primer caso, la fuente de tensión está aportando una energía eléctrica que se convierte en energía mecánica (ya que la barra se acelera), es decir, se comporta como un motor.
En el segundo caso, se reduce la energía mecánica, generándose una corriente eléctrica, por lo que el sistema funciona como un generador.
4 Disparo
En el caso planteado dbemeos resolver la ecuación de movimiento
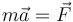
La velocidad, la aceleración y la fuerza van todas en la misma dirección, por lo que podemos usar cantidades escalares y escribirla como
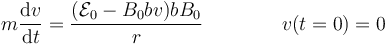
Para resolverla, sacamos factor común de algunos términos
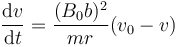
Dado que si la velocidad es menor que v0, la fuerza acelera a la barra, pero si es mayor la frena, concluimos que la barra tiende a moverse con velocidad v0. Por ello, podemos escribir la velocidad en cualquier instante como

En términos de esta variable u, la ecuación diferencial queda
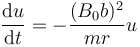
cuya solución es

La solución de la ecuación completa es entonces
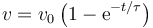
que, como en otros problemas similares (caída de un paracaidista, corriente en un circuito con resistencia y autoinducción,…) nos dice que la velocidad parte de 0 y tiende asintóticamente a un valor límite.
Eligiendo adecuadamente los valores de la tensión de la fuente, las dimensiones de la barra y los raíles y el campo magnético aplicado, pueden conseguirse velocidades muy elevadas, por lo que esto funciona como cañón electromagnético.





