Preguntas de test de campo magnético (GIE)
De Laplace
(→Espiras paralelas) |
(→Fuerza entre cargas en movimiento) |
||
| Línea 36: | Línea 36: | ||
===Solución=== | ===Solución=== | ||
La respuesta correcta es la '''<span style="color:red;">C<span>'''. | La respuesta correcta es la '''<span style="color:red;">C<span>'''. | ||
| + | |||
| + | El campo magnético debido a una carga en movimiento es | ||
| + | |||
| + | <center><math>\vec{B}_1 \simeq \frac{\mu_0 q_1 \vec{v}_1\times(\vec{r}-\vec{r}_1)}{|\vec{r}-\vec{r}_1|^3}</math></center> | ||
| + | |||
| + | Este campo se anula en los puntos donde <math>(\vec{r}-\vec{r}_1)</math> sea paralelo a <math>\vec{v}</math>, es decir, en los puntos de la recta de movimiento de la carga (hacia adonde apunta la velocidad). | ||
| + | |||
| + | En esta pregunta la carga 1 se mueve en la dirección del eje Z. Por tanto, el campo magnético en los puntos de este eje se anula. Puesto que la segunda carga se encuentra sobre este miesmo eje, el campo de la primera en la posición de esta segunda se anula | ||
| + | |||
| + | <center><math>\vec{B}_1(\vec{r}_2)=\frac{\mu_0}{4\pi}\,\frac{q_1(v_0\vec{k})\times(a\vec{k})}{a^3}=\vec{0}</math></center> | ||
| + | |||
| + | y por tanto se anula la fuerza magnética de la primera sobre la segunda | ||
| + | |||
| + | <center><math>\vec{F}_{1\to 2}=q_2\vec{v}_2\times\vec{B}_1(\vec{r}_2)=\vec{0}</math></center> | ||
| + | |||
| + | Lo mismo ocurre si se calcula la fuerza que la 2 produce sobre la 1. Por tanto, la fuerza entre ellas es nula en los dos casos. | ||
==Comparación de bobinas== | ==Comparación de bobinas== | ||
Revisión de 00:31 13 jun 2014
Contenido |
1 Espiras paralelas
Dos espiras circulares se sitúan de la manera indicada en la figura, con las intensidades de corriente en los sentidos que se indican. ¿Cómo es la interacción de la inferior sobre la superior?
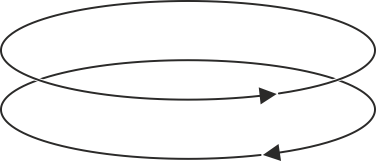
- A La atrae.
- B No ejerce ninguna interacción
- C La repele.
- D Aparece un par de fuerzas que tiende a darle la vuelta.
1.1 Solución
La respuesta correcta es la C.
Es una consecuencia inmediata de que corrientes antiparalelas (↑↓)se repelen.
Más en detalle, debemos considerar el campo magnético debido a una de las espiras, la de abajo por ejemplo. El campo debido a esta espira describe curvas cerradas (no circulares) alrededor de la espira, siendo el sentido de recorrido el dado por la regla de la mano derecha.
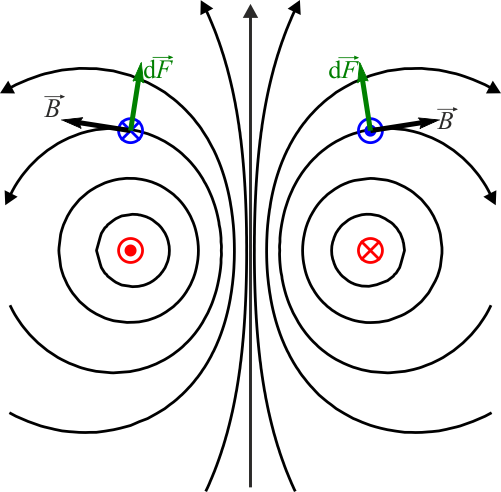
La segunda espira se encuentra inmersa en el campo de ésta. Sobre cada elemento de corriente se produce un diferencial de fuerza
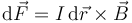
Esta fuerza diferencial es perpendicular a la corriente y al campo. Por la regla d ela mano derecha para el producto vectorial resulta una fuerza que va principalmente hacia arriba (aunque tiene una cierta inclinación). Cuando sumamos todos los diferenciales de fuerza para obtener la fuerza neta, las componentes horizontales se cancelan y resulta una fuerza vertical repulsiva.
Análogamente si calculamos el efecto de la espira superior sobre la inferior
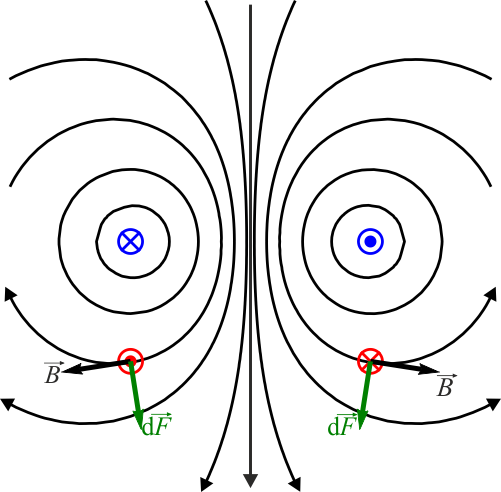
2 Fuerza entre cargas en movimiento
Dos cargas eléctricas iguales se mueven por el eje Z. En un instante dado una se encuentra en el origen moviéndose con 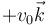 y la otra en
y la otra en 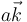 moviéndose con
moviéndose con 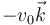 . ¿Cómo es la fuerza magnética entre las cargas?
. ¿Cómo es la fuerza magnética entre las cargas?
- A Atractiva.
- B Repulsiva.
- C Nula.
- D Perpendicular al eje Z.
2.1 Solución
La respuesta correcta es la C.
El campo magnético debido a una carga en movimiento es
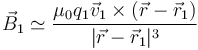
Este campo se anula en los puntos donde 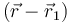 sea paralelo a
sea paralelo a  , es decir, en los puntos de la recta de movimiento de la carga (hacia adonde apunta la velocidad).
, es decir, en los puntos de la recta de movimiento de la carga (hacia adonde apunta la velocidad).
En esta pregunta la carga 1 se mueve en la dirección del eje Z. Por tanto, el campo magnético en los puntos de este eje se anula. Puesto que la segunda carga se encuentra sobre este miesmo eje, el campo de la primera en la posición de esta segunda se anula
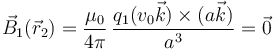
y por tanto se anula la fuerza magnética de la primera sobre la segunda

Lo mismo ocurre si se calcula la fuerza que la 2 produce sobre la 1. Por tanto, la fuerza entre ellas es nula en los dos casos.
3 Comparación de bobinas
¿Cuál de las siguientes bobinas produce un campo magnético más intenso en su interior cuando por ellas circula una corriente de 1 A?
- A Una de 300 vueltas, 15 cm de longitud y 2 cm de diámetro.
- B Una de 200 vueltas, 8 cm de longitud y 1 cm de diámetro.
- C Una de 500 vueltas, 30 cm de longitud y 2 cm de diámetro.
- D Una de 400 vueltas, 20 cm de longitud y 1 cm de diámetro.
3.1 Solución
La respuesta correcta es la B.
El campo magnético en el interior de una bobina es, aproximadamente
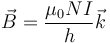
Dado que la corriente y μ0 son los mismos en todos los casos, y el radio no aparece en la fórmula, lo único que hay que comparar son las densidades de espiras N/h, que dan
- A: 300/15 = 20 vueltas/cm
- B: 200/8 = 25 vueltas/cm
- C: 500/30 = 16.7 vueltas/cm
- D: 400/20 = 20 vueltas/cm
luego el mayor campo se produce en la B, que es la que tiene mayor densidad de espiras.
4 Variación del radio de una espira
Se aumenta el radio de una espira circular por 4. ¿Por cuánto hay que multiplicar la corriente que circula por ella para que produzca el mismo campo magnético en su centro?
- A Es indiferente, porque el campo justo en el centro es nulo.
- B Por 4.
- C Por 2.
- D Por 16.
4.1 Solución
La respuesta correcta es la B.





