Dos esferas conductoras concéntricas
De Laplace
(→Caso general) |
|||
| Línea 32: | Línea 32: | ||
<center><math>V(r)=\begin{cases} \displaystyle\frac{Q}{4\pi\varepsilon_0 a} & r< a \\ & \\ \displaystyle\frac{Q}{4\pi\varepsilon_0 r} & r > a\end{cases}</math></center> | <center><math>V(r)=\begin{cases} \displaystyle\frac{Q}{4\pi\varepsilon_0 a} & r< a \\ & \\ \displaystyle\frac{Q}{4\pi\varepsilon_0 r} & r > a\end{cases}</math></center> | ||
| + | |||
| + | En este caso tenemos dos superficies cargadas. Una de radio <math>a</math> con una carga <math>Q_1</math> (diferente en cada caso) y una de radio <math>b</math> con una carga <math>Q_2</math>. Realmente tenemos tres, ya que la corteza exterior tiene dos caras, sin embargo, al ser muy fina, podemos considerar las dos caras como una sola superficie con carga total la suma de las dos caras. | ||
===Potenciales en función de las cargas=== | ===Potenciales en función de las cargas=== | ||
| + | Aplicando el resultado anterior tenemos, para el potencial de la esfera maciza | ||
| + | |||
| + | V_1 = \frac{Q_ | ||
===Cargas en función de los potenciales=== | ===Cargas en función de los potenciales=== | ||
===Circuito equivalente=== | ===Circuito equivalente=== | ||
===Energía electrostática=== | ===Energía electrostática=== | ||
| - | |||
==Análisis de los diferentes casos== | ==Análisis de los diferentes casos== | ||
[[Categoría:Problemas de electrostática en medios materiales (GIE)]] | [[Categoría:Problemas de electrostática en medios materiales (GIE)]] | ||
Revisión de 20:37 17 abr 2014
Contenido |
1 Enunciado
Se construye un sistema de dos conductores metálicos. El “1” es una esfera maciza de radio 6 cm. El “2” es una fina corona esférica, concéntrica con la anterior, de radio 9 cm. Halle la carga almacenada y el potencial al que se encuentra cada conductor, así como la energía almacenada en el sistema, para los siguientes casos:
- La esfera almacena una carga de +2 nC y la corona está aislada y descargada
- La esfera almacena una carga de +2 nC y la corona de +3 nC
- La esfera almacena una carga de −2 nC y la corona de +2 nC
- La esfera almacena una carga de −2 nC y la corona de +3 nC
- La esfera almacena una carga de +2 nC y la corona está a tierra
- La esfera está a tierra y la corona almacena una carga de +3 nC
- La esfera está a +200 V y la corona está a tierra.
- La esfera está a tierra y la corona a +200 V.
- La esfera y la corona están a +200 V
- La esfera está a +200 V y la corona está a −200 V.
Sugerencia: Resuélvase primero el caso general, estableciendo relaciones entre las cargas y los potenciales, y expresiones para la energía. Puede ser útil construir un circuito equivalente.
2 Introducción
Aunque este problema consta de muchos apartados, es fácil ver que todos son muy parecidos, sólo cambia el dato que se da y el valor de cada uno.
Éste es un caso particular de problema del potencial. Tenemos un sistema de conductores (dos, en este caso), que se encuentran en equilibrio electrostático. De cada conductor, sabemos que su potencial es el mismo en todos sus puntos, pero no necesariamente cuanto vale éste.
Para cada conductor hay que dar o bien su voltaje o bien su carga total (pero no como está distribuida ésta), nunca las dos cosas a la vez. Eso sería redundante o contradictorio. A partir de esta información se puede determinar las cargas o potenciales que se desconocen, resolviendo el problema del potencial.
En el caso de un sistema de dos conductores, el resultado es una relación lineal entre las cargas y los potenciales

Estos problemas se simplifican mucho mediante la construcción de circuitos equivalentes, donde cada par de superficies conductoras en influencia total se modela como un conductor.
3 Caso general
En este caso concreto, todas las superficies conductoras son esferas concéntricas. Dado que todas ellas son equipotenciales debemos preguntarnos qué distribución de carga produce un potencial uniforme sobre una esfera. La respuesta es sencilla: por la simetría del sistema, lo que tenemos son distribuciones de carga uniformes sobre cada superficie. Esto no sería cierto si tuviéramos esferas descentradas, por ejemplo.
Si las superficies esféricas están cargadas uniformemente, el problema es muy sencillo y ya ha sido resuelto en el tema de electrostática en el vacío. El potencial creado por una superficie cargada uniformemente es, para cualquier punto del espacio
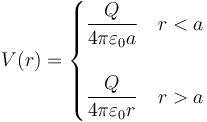
En este caso tenemos dos superficies cargadas. Una de radio a con una carga Q1 (diferente en cada caso) y una de radio b con una carga Q2. Realmente tenemos tres, ya que la corteza exterior tiene dos caras, sin embargo, al ser muy fina, podemos considerar las dos caras como una sola superficie con carga total la suma de las dos caras.
3.1 Potenciales en función de las cargas
Aplicando el resultado anterior tenemos, para el potencial de la esfera maciza
V_1 = \frac{Q_





