Deslizamiento de una placa triangular
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una placa en forma de triángulo rectángulo con catetos que miden <math>|\overrightarrow{AB}|=60\,\mathrm{cm}</math> y <math>|\overrightarrow{BC}|=80\,\mathrm{cm}…') |
|||
| Línea 19: | Línea 19: | ||
# El centro de masas, G, de un triángulo homogéneo es el baricentro, cuyas coordenadas son la media aritmética de las de los tres vértices. Calcule la velocidad y aceleración del CM para este mismo instante. ¿Qué trayectoria describe el baricentro? | # El centro de masas, G, de un triángulo homogéneo es el baricentro, cuyas coordenadas son la media aritmética de las de los tres vértices. Calcule la velocidad y aceleración del CM para este mismo instante. ¿Qué trayectoria describe el baricentro? | ||
| + | ==Introducción== | ||
| + | ==Velocidad de los vértices== | ||
| + | ==Velocidad angular== | ||
| + | ==Tipo de movimiento== | ||
| + | ==Eje instantáneo de rotación== | ||
| + | ==Aceleración de cada vértice== | ||
| + | ==Propiedades del CM== | ||
[[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | [[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | ||
Revisión de 19:19 11 ene 2014
Contenido |
1 Enunciado
Una placa en forma de triángulo rectángulo con catetos que miden 
y 
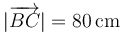desliza por dos paredes (XZ e YZ) y el suelo (XY) de forma que:
- Su vértice C desciende por la esquina entre las dos paredes (eje Z)
- Su vértice B se desliza por la esquina entre la pared del fondo y el suelo (eje Y).
- Su vértice A se desliza por el suelo, de forma que el vector de posición relativa
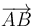es siempre paralelo a la esquina entre la pared lateral y el suelo.
Suponga que la velocidad del vértice B es constante,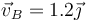 
(m/s)
En un determinado momento, el vértice B se encuentra a 64\,cm de la esquina. Para este instante:
- Calcule la velocidad de cada vértice.
- Halle la velocidad angular de la placa.
- Identifique el tipo de movimiento que describe el sólido (traslación, rotación,…)
- Dé la ecuación del EIRMD (o EIR, en su caso).
- Halle la aceleración de cada vértice.
- El centro de masas, G, de un triángulo homogéneo es el baricentro, cuyas coordenadas son la media aritmética de las de los tres vértices. Calcule la velocidad y aceleración del CM para este mismo instante. ¿Qué trayectoria describe el baricentro?
