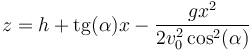Tiro parabólico con desnivel
De Laplace
(→Solución sin barrera) |
|||
| Línea 31: | Línea 31: | ||
<center><math> | <center><math> | ||
\left\{\begin{array}{rcl} x & = & v_0\cos(\alpha) t \\ && \\ z & = & h +v_0\,\mathrm{sen}(\alpha)t-\displaystyle\frac{1}{2}gt^2\end{array}\right.</math></center> | \left\{\begin{array}{rcl} x & = & v_0\cos(\alpha) t \\ && \\ z & = & h +v_0\,\mathrm{sen}(\alpha)t-\displaystyle\frac{1}{2}gt^2\end{array}\right.</math></center> | ||
| + | |||
| + | siendo <math>v_0</math> la rapidez inicial y <math>\alpha</math> el ángulo de lanzamiento respecto a la horizontal. | ||
Podemos eliminar el tiempo entre estas dos ecuaciones despejando en la primera y sustituyendo en la segunda. Queda la ecuación de la trayectoria parabólica | Podemos eliminar el tiempo entre estas dos ecuaciones despejando en la primera y sustituyendo en la segunda. Queda la ecuación de la trayectoria parabólica | ||
Revisión de 18:33 28 dic 2013
Contenido |
1 Enunciado
En una partida de los Angry Birds se debe lanzar un pájaro para alcanzar a un cerdo, siendo el movimiento del pájaro debido únicamente a la acción de la gravedad (se desprecia el rozamiento con el aire).
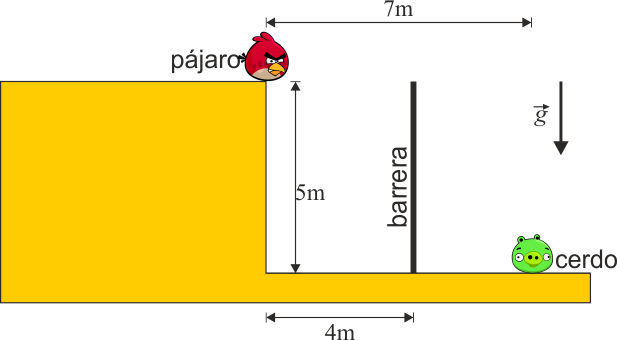
El tirachinas con el que se lanza el pájaro se encuentra a una altura de 5 m respecto al suelo en el que se halla el cerdo. Éste se encuentra a una distancia sobre la horizontal horizontal de 7 m del lanzador.
Entre el pájaro y el cerdo se encuentra una barrera de 5 m de altura, situada a 4 m del punto de lanzamiento.
Suponiendo que tanto el pájaro como el cerdo son objetos puntuales y que la barrera es de pequeño espesor, pero absolutamente rígida, calcule la rapidez y el ángulo de elevación respecto a la horizontal con los que debe lanzarse el pájaro, si la rapidez debe ser mínima. ¿Qué rapidez tiene el pájaro en el momento en que impacta con el cerdo? ¿Cuánto tarda en hacerlo? Tómese 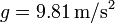 .
.
Suponga ahora que, por error, le comunicamos una rapidez mayor en un 5% a la que debería tener, pero manteniendo correcto el ángulo. ¿Cuánto más lejos o más cerca impacta el pájaro?
2 Introducción
A la hora de resolver este problema puede darse por sentado, demasiado a la ligera, que la trayectoria óptima es la que pasa rasante por la barrera, pero esto no tiene por qué ser así.
Imaginemos que la barrera, en lugar de estar a 4 m estuviera a solo 1 m. Es claro entonces que la mejor trayectoria esquivaría la barrera, pasando por encima de ella y sería lo mismo que si no estuviera.
Tenemos entonces que calcular la trayectoria de mínima rapidez y ver si pasa por encima de la barrera o choca con ella. Si es lo primero, ya habremos acabado, si es lo segundo habrá que calcular de nuevo empleando la trayectoria que pasa rasante.
3 Solución sin barrera
Supongamos, para hacerlo general, que el pájaro se encuentra a una altura z = h, y el cerdo a una distancia horizontal x = b del punto de lanzamiento.
Una vez que el pájaro es lanzado describe un movimiento parabólico
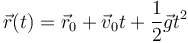
con las condiciones iniciales
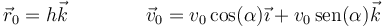
Separando en componentes nos quedan las ecuaciones horarias
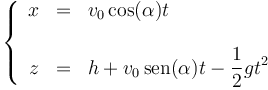
siendo v0 la rapidez inicial y α el ángulo de lanzamiento respecto a la horizontal.
Podemos eliminar el tiempo entre estas dos ecuaciones despejando en la primera y sustituyendo en la segunda. Queda la ecuación de la trayectoria parabólica