Preguntas de test de sistemas de partículas
De Laplace
(→Impacto horizontal sobre un bloque) |
(→Solución) |
||
| Línea 221: | Línea 221: | ||
Como la masa de la bala es muy pequeña comparada con la del bloque, puede despreciarse y aproximar el valor numérico del resultado | Como la masa de la bala es muy pequeña comparada con la del bloque, puede despreciarse y aproximar el valor numérico del resultado | ||
| - | <center><math>v_0 \simeq \frac{M}{m}V = \frac{1}{.004}\times 1\,\frac{\mathrm{m}}{\mathrm{s}} = 250\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | + | <center><math>v_0 \simeq \frac{M}{m}V = \frac{1}{0.004}\times 1\,\frac{\mathrm{m}}{\mathrm{s}} = 250\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> |
(un cálculo exacto da 248 m/s, bastante próximo a esta aproximación) | (un cálculo exacto da 248 m/s, bastante próximo a esta aproximación) | ||
Revisión de 14:01 7 dic 2013
Contenido |
1 Colisión tridimensional
Una proyectil de masa m que se mueve con velocidad 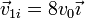 colisiona con un blanco inmóvil de masa 2m. El proyectil tiene tras la colisión una velocidad
colisiona con un blanco inmóvil de masa 2m. El proyectil tiene tras la colisión una velocidad 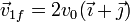 ¿Cuánto vale la velocidad final de la segunda masa?
¿Cuánto vale la velocidad final de la segunda masa?
- A
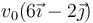 .
.
- B Es nula.
- C Depende de si la colisión es elástica o inelástica.
- D
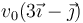 .
.
1.1 Solución
La respuesta correcta es la D.
En una colisión, elástica o inelástica, todas las fuerzas son internas, por lo que se conserva la cantidad de movimiento del sistema. Por tanto, para hallar la velocidad final de la segunda masa nos basta con igualar la cantidad de movimiento inicial a la final
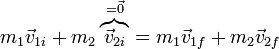
Despejando
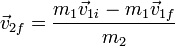
y sustituyendo

2 Arrastre de una masa
Se tiene un sistema de 2 masas de 4 kg cada una, atadas por una cuerda ideal, inextensible y sin masa, que pasa por una polea también ideal. La masa 1 está sobre una superficie horizontal sin rozamiento, mientras que la 2 cuelga verticalmente.
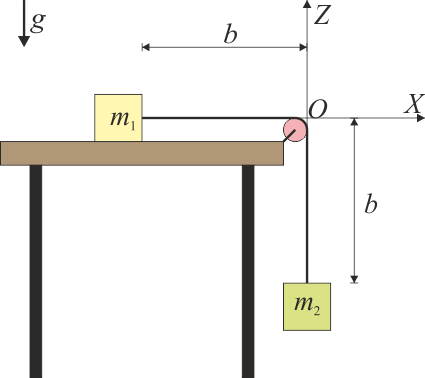
2.1 Pregunta 1
Suponiendo el sistema de ejes de la figura, ¿cuánto vale la aceleración de cada masa en el instante indicado, en m/s²?
- A
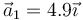 ,
, 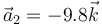
- B
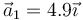 ,
, 
- C
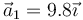 ,
, 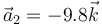
- D
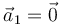 ,
, 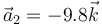
2.1.1 Solución
La respuesta correcta es la B.
Este es un caso particular de otro problema. Sobre la masa 1 actúan tres fuerzas: su peso, la reacción normal de la mesa y la tensión de la cuerda que tira de ella. Si hubiera rozamiento también deberíamos incluirlo, pero no es el caso. Por tanto tenemos
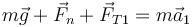
Para la segunda masa las únicas fuerzas que actúan son su peso y la tensión que tira de ella hacia arriba
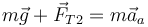
Separando en componentes cada una de estas ecuaciones tenemos, para la primera masa

ya que su aceleración es puramente horizontal. Para la segunda masa obtenemos una sola ecuación escalar
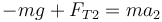
Por tratarse de un hilo ideal sin masa, el módulo de la tensión en el extremo de la masa 1 es igual al del otro extremo
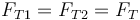
y por ser inextensible la rapidez y la aceleración horizontal de la masa 1 debe coincidir con la de la masa 2,

El signo negativo proviene de que, de acuerdo con el sistema de ejes elegido hemos considerado

es decir, ambas dirigidas hacia la polea, por lo que una de ellas debe ser negativa.
Con estas simplificaciones queda el sistema
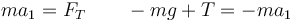
Sumando las dos ecuaciones hallamos las aceleraciones

y, en forma vectorial,

2.2 Pregunta 2
¿Cuál de las cuatro figuras representa correctamente la posición y velocidad del centro de masas C del sistema de dos pesas, en el instante representado?
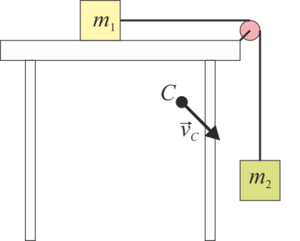
| 
|
| A | B |
|---|---|

| 
|
| C | D |
2.2.1 Solución
La respuesta correcta es la A.
El centro de masas es la media ponderada de las posiciones respectivas

para la posición y las masas de la figura

resulta la posición del CM
Este punto se halla sobre la recta que une las dos partículas (o, para ser precisos, sus respectivos centros de masas). Si además las dos masas son iguales, el centro de masas se halla en el punto medio entre ellas

Por tanto, la respuesta correcta solo puede ser la A o la D.
La velocidad del CM es también la media ponderada de las dos velocidades
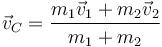
siendo las velocidades en este instante

Es indiferente el valor instantáneo de la velocidad. Debido a que la cuerda es inextensible, lo que avanza la masa sobre la mesa es igual a lo que desciende la que cuelga.
Esto da
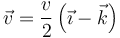
y por tanto la velocidad del CM tiene una dirección oblicua como ilustra la figura A.
2.3 Pregunta 3
¿Cuánto vale la aceleración del centro de masas en el mismo instante?
- A
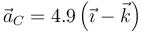
- B Es nula.
- C
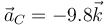
- D
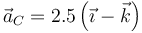
2.3.1 Solución
La respuesta correcta es la D.
De manera análoga a la posición y la velocidad hallamos la aceleración del centro de masas

que en este caso nos da
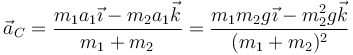
Al ser iguales las dos masas
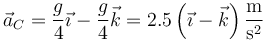
3 Centro de masas de una L
Se tiene un sólido en forma de L con los brazos de igual longitud h, siendo M la masa total del sólido, distribuida uniformemente.
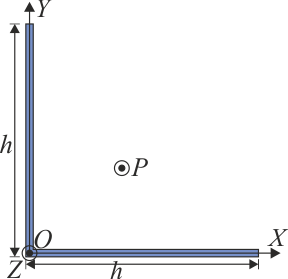
Considerando un sistema de ejes con origen en el vértice y ejes OX y OY paralelos a los brazos de la L, ¿dónde se encuentra en centro de masas del sólido?
- A En

- B En el origen de coordenadas.
- C En
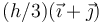
- D En
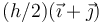
3.1 Solución
La respuesta correcta es la A.
Por la simetría del sistema, el CM debe hallarse sobre la bisectriz de la escuadra.
Además, debe encontrarse en la línea que une los centros de masas de cada uno de los brazos. Estos centros de masas están en los centros respectivos, por lo que el CM de la figura se halla en la recta que va de 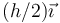 a
a  .
.
La intersección de esta recta con la bisectriz en el punto

4 Impacto horizontal sobre un bloque
Para medir una velocidad de un proyectil se dispara una bala de masa 4 gramos sobre un bloque de madera de 1 kg, inicialmente en reposo, quedándose la bala empotrada en él. El bloque reposa sobre una superficie horizontal, sobre la cual el coeficiente de rozamiento (estático y dinámico) es μ = 0.25. Como consecuencia del impacto, el bloque (con bala) se desliza una distancia de 20 cm hasta pararse.
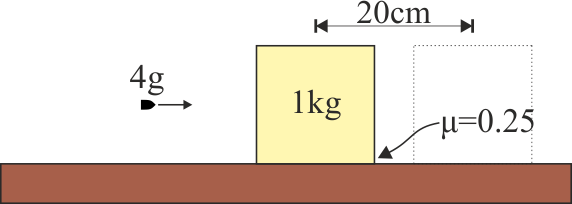
4.1 Pregunta 1
¿Qué velocidad tenía aproximadamente el bloque justo tras el impacto?
- A 2 m/s
- B 70 cm/s
- C 20 cm/s.
- D 1 m/s.
4.1.1 Solución
La respuesta correcta es la D.
El bloque (bala incluida) se desliza hasta que se le agota su energía cinética. Por el teorema de las fuerzas vivas
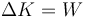
La variación de la energía cinética es

con V la velocidad justo tras el impacto.
El trabajo debido a la fuerza de rozamiento es igual al producto de la fuerza por la distancia recorrida
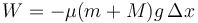
Igualando y despejando
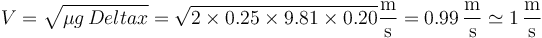
4.2 Pregunta 2
¿Qué velocidad llevaba la bala justo antes del impacto?
- A 500 m/s
- B 250 m/s
- C 50 m/s
- D 16 m/s
4.2.1 Solución
La respuesta correcta es la B.
En la colisión se conserva la cantidad de movimiento. Por tanto

y despejando

Como la masa de la bala es muy pequeña comparada con la del bloque, puede despreciarse y aproximar el valor numérico del resultado
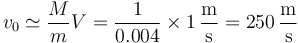
(un cálculo exacto da 248 m/s, bastante próximo a esta aproximación)
4.3 Pregunta 3
¿Qué proporción de la energía inicial se perdió en la colisión de la bala con el bloque?
- A 0.0%
- B 50.0%
- C 99.6%
- D 0.4%
4.3.1 Solución
La respuesta correcta es la C.
La energía cinética antes de la colisión es
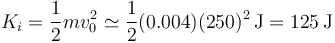
y la posterior
La proporción de energía perdida es
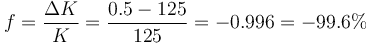
Se puede llegar a este resultado más rigurosamente y sin cálculos intermedios observando que
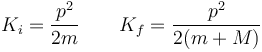
siendo p la cantidad de movimiento, igual antes y después de la colisión. Por tanto
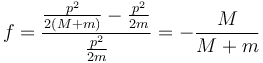
Esta fracción depende solo de la proporción entre las masas y no de cómo de rápida vaya la bala. Para proyectil muy ligeros comparados con el blanco, la proporción tiende al 100% como en este caso.
5 Explosión de un proyectil
Un proyectil de masa 4 kg se mueve horizontalmente con velocidad de 6 m/s. En un momento dado explota en dos fragmentos, uno de los cuales tiene una masa de 1 kg y sale despedido hacia atrás con velocidad −6 m/s.
5.1 Pregunta 1
¿Cuál es la velocidad del segundo fragmento tras la explosión?
- A 18 m/s
- B 6 m/s
- C 0 m/s
- D 10 m/s
5.1.1 Solución
La respuesta correcta es la C.
5.2 Pregunta 2
En este proceso la energía cinética del sistema…
- A Disminuye.
- B Permanece constante.
- C Cambia de signo.
- D Aumenta.
5.2.1 Solución
La respuesta correcta es la D.





