Equilibrios de un péndulo
De Laplace
(→Puntos de equilibrio) |
(→Curva de potencial) |
||
| Línea 24: | Línea 24: | ||
La gráfica de esta función es una sinusoide con el mínimo en <math>\theta=0</math>. En principio, la gráfica se extiende solo al rango <math>[-\pi,\pi]</math>. Sin embargo, para incluir la posibilidad de que el péndulo pueda superar la posición del máximo y dar vueltas completas, extendemos la gráfica a valores mayores de <math>\theta</math> por ambos extremos. | La gráfica de esta función es una sinusoide con el mínimo en <math>\theta=0</math>. En principio, la gráfica se extiende solo al rango <math>[-\pi,\pi]</math>. Sin embargo, para incluir la posibilidad de que el péndulo pueda superar la posición del máximo y dar vueltas completas, extendemos la gráfica a valores mayores de <math>\theta</math> por ambos extremos. | ||
| - | <center>[[Archivo:energia-pendulo.png]]</center> | + | <center>[[Archivo:energia-pendulo-02.png]]</center> |
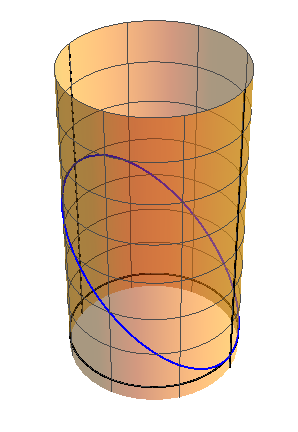
| + | Una forma más correcta, pero más difícil de ver, sería “enrollar” la gráfica de forma que el ángulo −π coincida con π. En esta gráfica, la curva de potencial tiene forma de una elipse trazada sobre un cilindro. | ||
| + | <center>[[Archivo:energia-pendulo-03.png]]</center> | ||
==Puntos de equilibrio== | ==Puntos de equilibrio== | ||
Revisión de 19:00 3 dic 2013
Contenido |
1 Enunciado
Trace la curva de energía potencial para un péndulo rígido de longitud L del que cuelga una masa m, en función del ángulo θ con el que se separa de la vertical. Suponga que el punto más bajo corresponda a U = 0. A la vista de la curva,
- ¿Qué puntos de equilibrio existen? ¿Son estables o inestables?
- ¿Cómo es el movimiento si la energía mecánica vale mgL? ¿Y si vale 3mgL?
2 Curva de potencial
La lenteja del péndulo está sometida a dos fuerzas: el peso y la tensión de la barra.
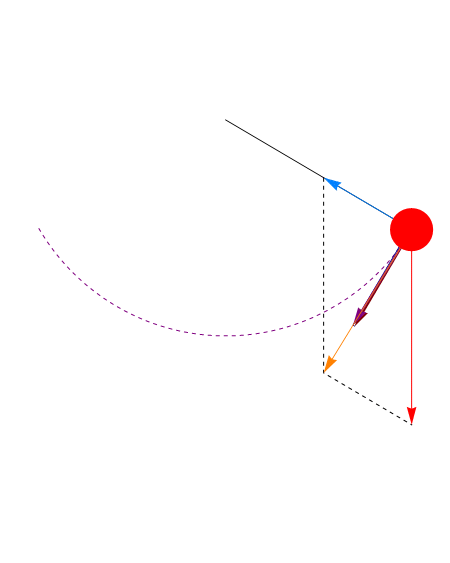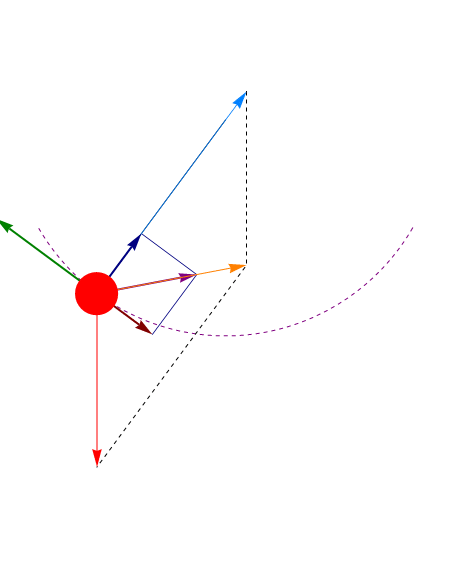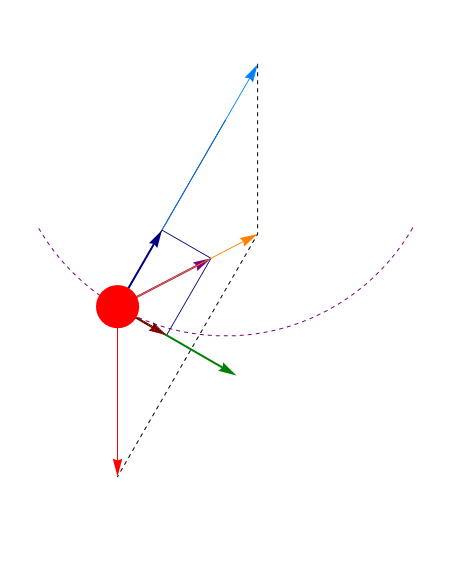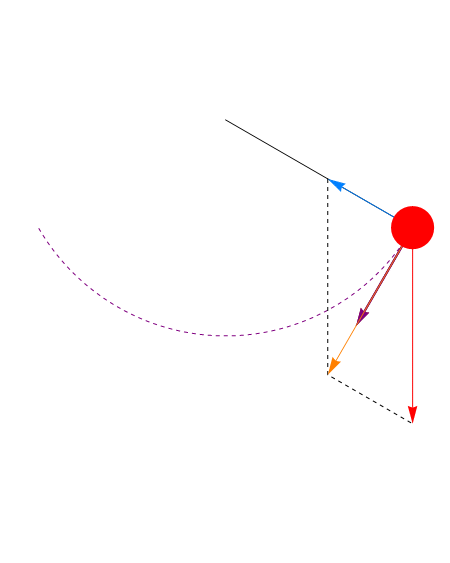
La tensión es siempre perpendicular al desplazamiento (ya que el desplazamiento es a lo largo de una circunferencia, mientras que la tensión es radial), por ello no realiza ningún trabajo y no influye en la conservación de la energía.
Por tanto, la única energía potencial es la gravitatoria
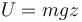
La altura z la podemos poner en función del ángulo que el péndulo forma con la vertical. Si tomamos como referencia de alturas el punto más bajo del péndulo, la altura en el momento que forma un ángulo \theta con la vertical es
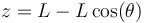
por lo que la energía potencial puede escribirse en la forma
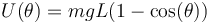
La gráfica de esta función es una sinusoide con el mínimo en θ = 0. En principio, la gráfica se extiende solo al rango [ − π,π]. Sin embargo, para incluir la posibilidad de que el péndulo pueda superar la posición del máximo y dar vueltas completas, extendemos la gráfica a valores mayores de θ por ambos extremos.
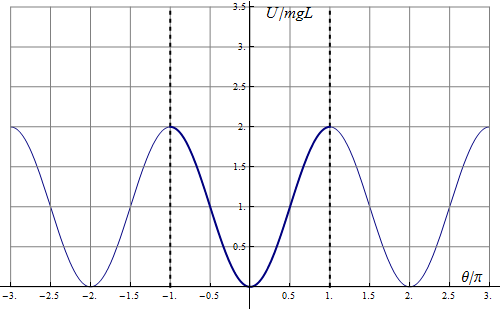
Una forma más correcta, pero más difícil de ver, sería “enrollar” la gráfica de forma que el ángulo −π coincida con π. En esta gráfica, la curva de potencial tiene forma de una elipse trazada sobre un cilindro.