Fuerza sobre tres masas yuxtapuestas
De Laplace
(Página creada con '== Enunciado == Tres masas <math>m_1</math>, <math>m_2 </math> y <math>m_3 </math> se encuentran yuxtapuestas sobre una superficie horizontal sin rozamiento. Sobre la primera d…')
Edición más nueva →
Revisión de 17:44 30 oct 2013
Contenido |
1 Enunciado
Tres masas m1, m2 y m3 se encuentran yuxtapuestas sobre una superficie horizontal sin rozamiento. Sobre la primera de ellas actúa una fuerza horizontal F. Calcula
- La aceleración de las masas.
- La fuerza resultante sobre cada una de ellas.
- Las magnitudes de las fuerzas de contacto entre ellas.
2 Solución
2.1 Aceleración de las masas
Si durante el movimiento de las masas se mantienen juntas, se pueden considerar una única partícula de masa m1 + m2 + m3. Las tres masas se mueven con la misma aceleración, por lo que la Segunda Ley de Newton nos dice

2.2 Fuerza neta sobre cada masa
Teniendo en cuenta que la aceleración de las tres masas es la misma, podemos aplicar la Segunda Ley de Newton a cada una de ellas para obtener la fuerza neta sobre cada masa
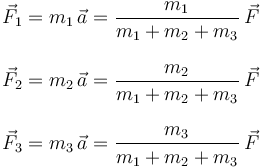
2.3 Fuerzas de contacto
Ahora consideramos las tres masas como partículas independientes. Las fuerzas que actúan sobre cada una de ellas son
Masa m1
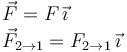
Masa m2
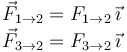
Masa m3
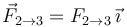
Además, aplicando la tercera Ley de Newton sabemos que las fuerzas mutuas entre dos masas son iguales en módulo y dirección y de sentido contrario

Las tres masas se mueven con la misma aceleración, por lo que aplicando la Segunda ley a cada una de ellas tenemos

De cada una de estas expresiones podemos despejar las fuerzas entre masas