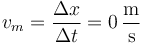Calculo de magnitudes a partir de v(t)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una partícula se mueve a lo largo de una recta de forma que su velocidad sigue la ley, en el SI <center><math>v(t) = (3t^2-66t+216)\,\frac{\mathrm{m}}{\mathrm{s}…') |
|||
| Línea 13: | Línea 13: | ||
# Los valores máximo y mínimo de la velocidad y la rapidez. | # Los valores máximo y mínimo de la velocidad y la rapidez. | ||
==Posición== | ==Posición== | ||
| + | La posición instantánea la hallamos integrando la velocidad | ||
| + | |||
| + | <center><math>x(t) = x_0+\int_0^t v(t)\,\mathrm{d}t</math></center> | ||
| + | |||
| + | En este caso | ||
| + | |||
| + | <center><math>x(t) = \int_0^t(3t^2-66t + 216)\mathrm{d}t = t^3 - 33t^2 + 216t</math></center> | ||
| + | |||
| + | estando el tiempo medido en segundos y la posición en metros. | ||
| + | |||
==Velocidad media== | ==Velocidad media== | ||
| + | El desplazamiento en este intervalo es | ||
| + | |||
| + | <center><math>\Delta x = x(24)-x(0) = 0 - 0 = 0\,\mathrm{m}</math></center> | ||
| + | |||
| + | con lo que la velocidad media es nula | ||
| + | |||
| + | <center><math>v_m = \frac{\Delta x}{\Delta t}=0\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
==Posición máxima y mínima== | ==Posición máxima y mínima== | ||
==Distancia recorrida y rapidez media== | ==Distancia recorrida y rapidez media== | ||
Revisión de 21:36 29 oct 2013
Contenido |
1 Enunciado
Una partícula se mueve a lo largo de una recta de forma que su velocidad sigue la ley, en el SI
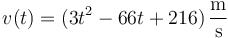
entre  y
y 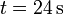 . La posición inicial es
. La posición inicial es  . Halle:
. Halle:
- La posición de la partícula en cada instante del intervalo indicado.
- La velocidad media de la partícula en este intervalo.
- Los valores máximo y mínimo de x.
- La distancia recorrida en ese intervalo y la rapidez media.
- La aceleración en todo instante.
- Los valores máximo y mínimo de la velocidad y la rapidez.
2 Posición
La posición instantánea la hallamos integrando la velocidad
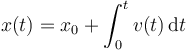
En este caso
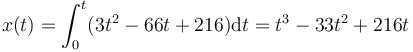
estando el tiempo medido en segundos y la posición en metros.
3 Velocidad media
El desplazamiento en este intervalo es
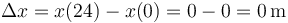
con lo que la velocidad media es nula