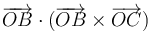Entrar Página Discusión Historial Go to the site toolbox

Preguntas de test de herramientas matemáticas (GIE)

De Laplace

(Diferencias entre revisiones)
(Página creada con ' ==Suma de vectores ligados== Dados los vectores ligados de la figura, <center>Archivo:suma-ligados-0.png</center> ¿cuánto vale su suma vectorial? {| class="bordeado" |…')

Revisión de 20:55 26 oct 2013

Contenido

1 Suma de vectores ligados

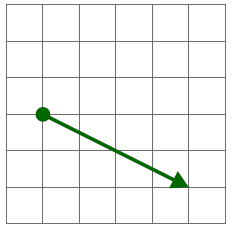
Dados los vectores ligados de la figura,

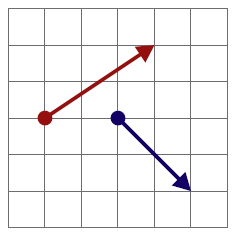
Archivo:suma-ligados-0.png

¿cuánto vale su suma vectorial?

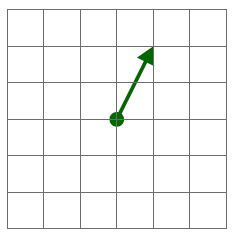
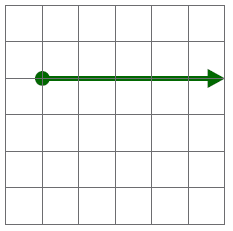
Archivo:suma-ligados-1.png Archivo:suma-ligados-2.png
A B
Archivo:suma-ligados-3.png Archivo:suma-ligados-4.png
C D

2 Ángulo entre dos vectores

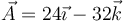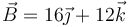¿Qué ángulo forman los vectores \vec{A}=24\vec{\imath}-32\vec{k} y \vec{B}=16\vec{\jmath}+12\vec{k}?

  • A 0.00 rad
  • B 1.07 rad
  • C 1.57 rad
  • D 2.07 rad

3 Posible igualdad vectorial

Si \vec{A} y \vec{B} son dos vectores unitarios, indique cuándo se cumple la igualdad

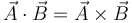
\vec{A}\cdot\vec{B} = \vec{A}\times\vec{B}
  • A Cuando \vec{A} y \vec{B} son paralelos.
  • B Cuando \vec{A} y \vec{B} son ortogonales.
  • C No se cumple nunca.
  • D Cuando \vec{A} y \vec{B} forman un ángulo de 45°.

4 Otra posible igualdad vectorial

Sean \vec{A}, \vec{B} y \vec{C} vectores arbitrarios no nulos. ¿Cuál de las siguientes afirmaciones es cierta siempre?

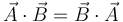
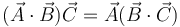
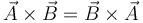
  • A \vec{A}\cdot\vec{B} = \vec{B}\cdot\vec{A}
  • B (\vec{A}\cdot\vec{B})\vec{C} = \vec{A}(\vec{B}\cdot\vec{C})
  • C \vec{A}\times\vec{B} = \vec{B}\times\vec{A}
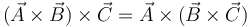
  • D (\vec{A}\times\vec{B})\times\vec{C} = \vec{A}\times(\vec{B}\times\vec{C})

5 Área de un triángulo

Dados tres puntos del espacio A, B y C, siendo O el origen de coordenadas, ¿cómo podemos hallar el área del triángulo que definen?

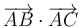
  • A \overrightarrow{AB}\cdot\overrightarrow{AC}
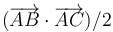
  • B (\overrightarrow{AB}\cdot\overrightarrow{AC})/2
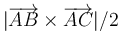
  • C |\overrightarrow{AB}\times\overrightarrow{AC}|/2
  • D \overrightarrow{OB}\cdot(\overrightarrow{OB}\times\overrightarrow{OC})
Obtenido de "http://tesla.us.es/wiki/index.php/Preguntas_de_test_de_herramientas_matem%C3%A1ticas_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace