Campo y carga de un potencial conocido
De Laplace
(→Densidad de carga) |
(→Volumétrica) |
||
| Línea 38: | Línea 38: | ||
Para hallar esta cantidad volvemos a descomponer en los dos semiespacios. Para <math>y > 0</math> tenemos | Para hallar esta cantidad volvemos a descomponer en los dos semiespacios. Para <math>y > 0</math> tenemos | ||
| - | <center><math>\mathbf{E} = V_0k\mathrm{e}^{-ky}\left(cos(kx)\mathbf{u}_x | + | <center><math>\mathbf{E} = V_0k\left(\mathrm{e}^{-ky}\mathrm{sen}(kx)\mathbf{u}_x+\mathrm{e}^{-ky}\cos(kx)\mathbf{u}_y\right)</math></center> |
| + | |||
| + | |||
| + | <center><math>\rho = \varepsilon_0 V_0 k \left(k\mathrm{e}^{-ky}\cos(kx)-k\mathrm{e}^{-ky}\cos(kx)\right) = 0</math></center> | ||
| + | |||
| + | y para <math>y < 0</math> | ||
| + | |||
| + | <center><math>\mathbf{E} = V_0k\left(\mathrm{e}^{ky}\mathrm{sen}(kx)\mathbf{u}_x-\mathrm{e}^{ky}\cos(kx)\mathbf{u}_y\right)</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\rho = \varepsilon_0 V_0 k \left(k\mathrm{e}^{ky}\cos(kx)-k\mathrm{e}^{ky}\cos(kx)\right) = 0</math></center> | ||
| + | |||
| + | Por tanto, la densidad de carga de volumen es nula en todos los puntos del espacio. Puesto que el campo no es nulo, y además se anula en el infinito, es claro que debe haber alguna densidad de carga adicional. Esta densidad es la superficial, que se encuentra en las superficies donde el campo es discontinuo. | ||
====Superficial==== | ====Superficial==== | ||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
Revisión de 13:36 26 nov 2008
Contenido |
1 Enunciado
El potencial eléctrico en todos los puntos del espacio viene dado por la ecuación
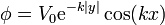
con k y V0 constantes.
- Halle el campo eléctrico en todos los puntos del espacio.
- Calcule la densidad de carga que crea este campo eléctrico.
2 Solución
2.1 Campo eléctrico
Para calcular el campo debemos hallar el gradiente del potencial, cambiado de signo.
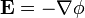
Para esto es conveniente separa el potencial en dos regiones
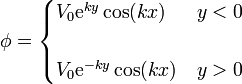
Hallando ahora el gradiente en cada región tenemos,
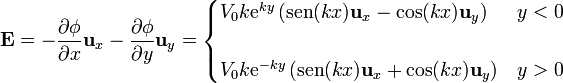
o, agrupando los dos casos
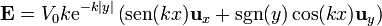
2.2 Densidad de carga
2.2.1 Volumétrica
La densidad de carga de volumen la obtenemos por aplicación de la ley de Gauss en forma diferencial
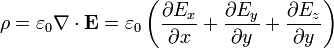
Para hallar esta cantidad volvemos a descomponer en los dos semiespacios. Para y > 0 tenemos
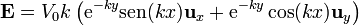
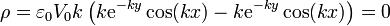
y para y < 0

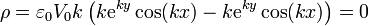
Por tanto, la densidad de carga de volumen es nula en todos los puntos del espacio. Puesto que el campo no es nulo, y además se anula en el infinito, es claro que debe haber alguna densidad de carga adicional. Esta densidad es la superficial, que se encuentra en las superficies donde el campo es discontinuo.





