Leyes del magnetismo (GIE)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Ley de Ampère== ==Ley de Gauss para el campo magnético== Categoría:Campo magnético (GIE)') |
(→Ley de Ampère) |
||
| Línea 1: | Línea 1: | ||
==Ley de Ampère== | ==Ley de Ampère== | ||
| + | Cuando se calcula el campo magnético debido a un hilo rectilíneo por el cual circula una intensidad de corriente <math>I</math> se llega al resultado | ||
| + | |||
| + | <center><math>\vec{B}=\frac{\mu_0 I}{2\pi\rho}\vec{u}_\varphi</math></center> | ||
| + | |||
| + | siendo <math>\rho</math> la distancia perpendicular al hilo y <math>\vec{u}_\varphi</math> el vector unitario acimutal. De esta expresión se deduce que las líneas de campo magnético son circunferencias que dan vueltas en torno al hilo de corriente. | ||
| + | |||
| + | Si ahora calculamos la circulación a lo largo de una de estas circunferencias, el resultado es independiente de la distancia al hilo | ||
| + | |||
| + | <center><math>\oint \vec{B}\cdot\mathrm{d}\vec{r} = \int_0^{2\pi}\left(\frac{\mu_0 I}{2\pi\rho}\vec{u}_\varphi\right)\cdot(\rho\,\mathrm{d}\varphi\vec{u}_\varphi) = \mu_0I</math></center> | ||
| + | |||
| + | Este resultado se puede generalizar a cualquier curva cerrada que envuelva una vez al hilo de corriente. Por contra, si consideramos una curva por el exterior del hilo, puede demostrarse que se anula la circulación del campo magnético. | ||
| + | |||
==Ley de Gauss para el campo magnético== | ==Ley de Gauss para el campo magnético== | ||
[[Categoría:Campo magnético (GIE)]] | [[Categoría:Campo magnético (GIE)]] | ||
Revisión de 09:46 20 may 2013
1 Ley de Ampère
Cuando se calcula el campo magnético debido a un hilo rectilíneo por el cual circula una intensidad de corriente I se llega al resultado
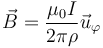
siendo ρ la distancia perpendicular al hilo y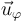 
el vector unitario acimutal. De esta expresión se deduce que las líneas de campo magnético son circunferencias que dan vueltas en torno al hilo de corriente.
Si ahora calculamos la circulación a lo largo de una de estas circunferencias, el resultado es independiente de la distancia al hilo
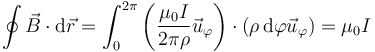
Este resultado se puede generalizar a cualquier curva cerrada que envuelva una vez al hilo de corriente. Por contra, si consideramos una curva por el exterior del hilo, puede demostrarse que se anula la circulación del campo magnético.
