Fuerzas magnéticas (GIE)
De Laplace
(→Fuerza de Lorentz) |
(→Fuerza de Lorentz) |
||
| Línea 1: | Línea 1: | ||
==Fuerza de Lorentz== | ==Fuerza de Lorentz== | ||
| + | ===Expresión=== | ||
Según se ve en el tema de ''[[Principios_de_la_electrostática_(GIE)#Campo_el.C3.A9ctrico|electrostática]]'', la fuerza eléctrica sobre una carga puntual en reposo viene dada por | Según se ve en el tema de ''[[Principios_de_la_electrostática_(GIE)#Campo_el.C3.A9ctrico|electrostática]]'', la fuerza eléctrica sobre una carga puntual en reposo viene dada por | ||
| Línea 19: | Línea 20: | ||
Esta expresión, que es válida en general, tanto para situaciones estáticas como dinámicas, se denomina ''Fuerza de Lorentz''. | Esta expresión, que es válida en general, tanto para situaciones estáticas como dinámicas, se denomina ''Fuerza de Lorentz''. | ||
| + | |||
| + | ===Trabajo magnético nulo=== | ||
| + | Una propiedad característica de la fuerza magnética sobre una carga magnética es que no realiza trabajo, por siempre normal a la velocidad. | ||
| + | |||
| + | <center><math>W = \int \vec{F}_m\cdot\mathrm{d}\vec{r}=\int(q\vec{v}\times\vec{B})\cdot(\vec{v}\mathrm{d}t)= q\int\vec{v}\cdot(\vec{v}\times\vec{B})\,\mathrm{d}t)=0</math></center> | ||
| + | |||
| + | y por tanto permanece constante la energía cinética de una carga que se mueve en un campo magnético. | ||
| + | |||
| + | En términos de las componentes intrínsecas de la aceleración, tenemos que la fuerza es siempre normal a la velocidad y por tanto la aceleración tangencial es siempre nula | ||
| + | |||
| + | <center><math>\vec{F}_m=q\vec{v}\times\vec{B}\perp\vec{v}</math>{{tose}}<math>a_t=0\,</math></center> | ||
| + | |||
| + | Si la aceleración tangencial es nula, la rapidez (módulo de la velocidad) permanece constante | ||
| + | |||
| + | <center><math>0=a_t=\frac{\mathrm{d}v}{\mathrm{d}t}</math>{{tose}}<math>v=|\vec{v}|=\mathrm{cte}</math></center> | ||
| + | |||
| + | Una rapidez constante implica una energía cinética constante. | ||
| + | |||
| + | Esto quiere decir que una carga puntual que se mueve en el seno de un campo magnético podrá cambiar de dirección de la velocidad (esto es, su movimiento sí será acelerado), pero no se moverá ni más rápido ni más lento en ningún momento. | ||
| + | |||
| + | Hay que destacar que esta conclusión, que el campo magnético no realiza trabajo, es sólo cierta para una carga puntual sometida a la fuerza de Lorentz. Si tenemos una corriente eléctrica (formada por millones de partículas en movimiento) o un dipolo magnético (que también experimenta fuerzas magnéticas) no es cierto que la energía cinética permanezca constante. De hecho, los [[freno magnético|frenos magnéticos]] se basan en la disminución de la energía cinética por acción de un campo magnético. | ||
==Fuerza sobre una corriente lineal== | ==Fuerza sobre una corriente lineal== | ||
Revisión de 20:01 12 may 2013
Contenido |
1 Fuerza de Lorentz
1.1 Expresión
Según se ve en el tema de electrostática, la fuerza eléctrica sobre una carga puntual en reposo viene dada por
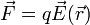
Sin embargo, si dicha carga se encuentra en movimiento, la experiencia muestra que se ve sometida a una fuerza adicional. Esta fuerza, que llamaremos fuerza magnética, verifica que es:
- Proporcional a la carga
- Proporcional al módulo de su velocidad
- Perpendicular a la velocidad
Con estas condiciones, la fuerza magnética debe ser de la forma
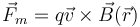
siendo  un nuevo campo, conocido como campo magnético. La fuerza total sobre una carga puntual es entonces
un nuevo campo, conocido como campo magnético. La fuerza total sobre una carga puntual es entonces
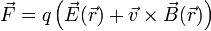
Esta expresión, que es válida en general, tanto para situaciones estáticas como dinámicas, se denomina Fuerza de Lorentz.
1.2 Trabajo magnético nulo
Una propiedad característica de la fuerza magnética sobre una carga magnética es que no realiza trabajo, por siempre normal a la velocidad.
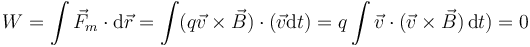
y por tanto permanece constante la energía cinética de una carga que se mueve en un campo magnético.
En términos de las componentes intrínsecas de la aceleración, tenemos que la fuerza es siempre normal a la velocidad y por tanto la aceleración tangencial es siempre nula
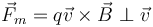

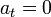
Si la aceleración tangencial es nula, la rapidez (módulo de la velocidad) permanece constante
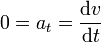

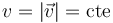
Una rapidez constante implica una energía cinética constante.
Esto quiere decir que una carga puntual que se mueve en el seno de un campo magnético podrá cambiar de dirección de la velocidad (esto es, su movimiento sí será acelerado), pero no se moverá ni más rápido ni más lento en ningún momento.
Hay que destacar que esta conclusión, que el campo magnético no realiza trabajo, es sólo cierta para una carga puntual sometida a la fuerza de Lorentz. Si tenemos una corriente eléctrica (formada por millones de partículas en movimiento) o un dipolo magnético (que también experimenta fuerzas magnéticas) no es cierto que la energía cinética permanezca constante. De hecho, los frenos magnéticos se basan en la disminución de la energía cinética por acción de un campo magnético.





