Fuerzas magnéticas (GIE)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Fuerza de Lorentz== ==Fuerza sobre una corriente lineal== ===Rectilínea=== ===De forma arbitraria=== ==Fuerza y par sobre una espira== ===Fuerza=== ===Par=== ===Momento magn…') |
(→Fuerza de Lorentz) |
||
| Línea 1: | Línea 1: | ||
==Fuerza de Lorentz== | ==Fuerza de Lorentz== | ||
| + | Según se ve en el tema de ''[[Principios_de_la_electrostática_(GIE)#Campo_el.C3.A9ctrico|electrostática]]'', la fuerza eléctrica sobre una carga puntual en reposo viene dada por | ||
| + | |||
| + | <center><math>\vec{F}=q\vec{E}(\vec{r})</math></center> | ||
| + | |||
| + | Sin embargo, si dicha carga se encuentra en movimiento, la experiencia muestra que se ve sometida a una fuerza adicional. Esta fuerza, que llamaremos ''fuerza magnética'', verifica que es: | ||
| + | |||
| + | * Proporcional a la carga | ||
| + | * Proporcional al módulo de su velocidad | ||
| + | * Perpendicular a la velocidad | ||
| + | |||
| + | Con estas condiciones, la fuerza magnética debe ser de la forma | ||
| + | |||
| + | <center><math>\vec{F}_m=q\vec{v}\times\vec{B}(\vec{r})</math></center> | ||
| + | |||
| + | siendo <math>\vec{B}</math> un nuevo campo, conocido como '''campo magnético'''. La fuerza total sobre una carga puntual es entonces | ||
| + | |||
| + | <center><math>\vec{F}=q\left(\vec{E}(\vec{r})+\vec{v}\times\vec{B}(\vec{r})\right)</math></center> | ||
| + | |||
| + | Esta expresión, que es válida en general, tanto para situaciones estáticas como dinámicas, se denomina ''Fuerza de Lorentz''. | ||
| + | |||
==Fuerza sobre una corriente lineal== | ==Fuerza sobre una corriente lineal== | ||
===Rectilínea=== | ===Rectilínea=== | ||
Revisión de 19:55 12 may 2013
Contenido |
1 Fuerza de Lorentz
Según se ve en el tema de electrostática, la fuerza eléctrica sobre una carga puntual en reposo viene dada por
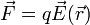
Sin embargo, si dicha carga se encuentra en movimiento, la experiencia muestra que se ve sometida a una fuerza adicional. Esta fuerza, que llamaremos fuerza magnética, verifica que es:
- Proporcional a la carga
- Proporcional al módulo de su velocidad
- Perpendicular a la velocidad
Con estas condiciones, la fuerza magnética debe ser de la forma
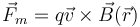
siendo 
un nuevo campo, conocido como campo magnético. La fuerza total sobre una carga puntual es entonces
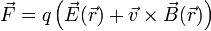
Esta expresión, que es válida en general, tanto para situaciones estáticas como dinámicas, se denomina Fuerza de Lorentz.
