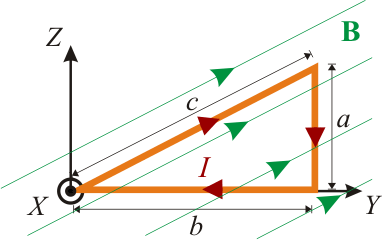
Espira triangular sometida a campo uniforme (F2GIA)

De Laplace

(Diferencias entre revisiones)

Revisión de 18:03 28 abr 2013

1 Enunciado

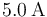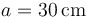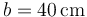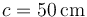Una espira de corriente que transporta una corriente de $5.0\,\mathrm{A}$ tiene forma de triángulo rectángulo con lados $a=30\,\mathrm{cm}$ , $b=40\,\mathrm{cm}\,$ y $c=50 \,\mathrm{cm}$ . Se sitúa la espira en una región donde existe un campo magnético uniforme de magnitud 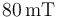$80\,\mathrm{mT}$ y cuya dirección es paralela al lado

c

. Calcular:

Fuerza ejercida por el campo magnético sobre cada lado de la espira.
Momento dipolar magnético de la espira.
Módulo del par ejercido por el campo magnético sobre la espira de corriente.

2 Solución

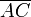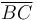Tomamos un sistema de referencia cartesiano tal que la espira $Γ$ de vértices $A$ , $B$ y $C$ , están contenida en un plano paralelo al $O Y Z$ , con los catetos $\overline{AC}$ y $\overline{BC}$ dispuestos paralelamente a los ejes $O Y$ y $O Z$ , respectivamente. La espira está sometida a un campo magnético uniforme (constante en todos los puntos del espacio), paralelo a la hipotenusa $\overline{AB}$ , y de módulo conocido:

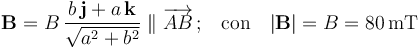
$\mathbf{B}=B\!\ \frac{b\!\ \mathbf{j}+a\!\ \mathbf{k}}{\sqrt{a^2+b^2}}\; \|\; \overrightarrow{AB}\!\ \mathrm{;}\quad \mbox{con}\quad|\mathbf{B}|=B=80\,\mathrm{mT}\,$

Cuando la espira es recorrida por una intensidad de corriente 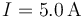$I=5.0\,\mathrm{A}\,$ , sobre los elementos de corriente 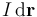$I\,\mathrm{d}\mathbf{r}$ definidos en cada uno de sus puntos, se ejercen fuerzas infinitesimales que, al sumarlas todas, producen una resultante nula:

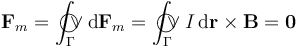
$\mathbf{F}_m=\int_{\Gamma}\!\!\!\!\!\!\bigcirc\!\!\!\!\vee \mathrm{d}\mathbf{F}_m=\int_{\Gamma}\!\!\!\!\!\!\bigcirc\!\!\!\!\vee I\,\mathrm{d}\mathbf{r}\times\mathbf{B}=\mathbf{0}$

Podemos comprobar que se cumple este resultado si calculamos las fuerzas sobre cada uno de los dados de la espira y luego los sumamos:

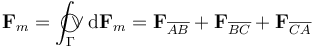
$\mathbf{F}_m=\int_{\Gamma}\!\!\!\!\!\!\bigcirc\!\!\!\!\vee \mathrm{d}\mathbf{F}_m=\mathbf{F}_{\overline{AB}}+\mathbf{F}_{\overline{BC}}+\mathbf{F}_{\overline{CA}}$

2.1 Fuerzas sobre cada lado de la espira

Obsérvese que, al estar formada por segmentos rectilíneos, el elemento de corriente en cada lado de la espira es colineal con el lado correspondiente; el sentido estará determinado por el sentido de la corriente. De esta forma, en el lado $\overline{AB}$ , se tendrá:

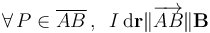
$\forall\,P\in\overline{AB}\,\mathrm{,}\,\;\;I\,\mathrm{d}\mathbf{r}\|\overrightarrow{AB}\|\mathbf{B}$

los elementos de corriente son colineales con el lado de la espira corriente en cada lado de la espira tiene la dirección

@@ Línea 24: / Línea 24: @@
 ===Fuerzas sobre cada lado de la espira===
+Obsérvese que, al estar formada por segmentos rectilíneos, el elemento de corriente en cada lado de la espira es colineal con el lado correspondiente; el sentido estará determinado por el sentido de la corriente. De esta forma, en el lado <math>\overline{AB}</math>, se tendrá:
+<math>\forall\,P\in\overline{AB}\,\mathrm{,}\,\;\;I\,\mathrm{d}\mathbf{r}\|\overrightarrow{AB}\|\mathbf{B}</math>
+los elementos de corriente son colineales con el lado de la espira corriente en cada lado de la espira tiene la dirección

Espira triangular sometida a campo uniforme (F2GIA)

De Laplace

Revisión de 18:03 28 abr 2013

1 Enunciado

2 Solución

2.1 Fuerzas sobre cada lado de la espira

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES