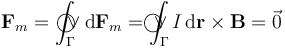Espira triangular sometida a campo uniforme (F2GIA)
De Laplace
(Diferencias entre revisiones)
(→Solución) |
(→Solución) |
||
| Línea 16: | Línea 16: | ||
<center><math>\,\mathrm{d}\mathbf{F}_m=I\,\mathrm{d}\mathbf{r}\times\mathbf{B}</math></center> | <center><math>\,\mathrm{d}\mathbf{F}_m=I\,\mathrm{d}\mathbf{r}\times\mathbf{B}</math></center> | ||
| - | <center><math>\mathbf{F}_m=\int_{\Gamma} | + | <center><math>\mathbf{F}_m=\int_{\Gamma}\!\!\!\!\!\!\!\bigcirc\!\!\!\!\vee |
\mathrm{d}\mathbf{F}_m=\int_{\Gamma}\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\!\vee I\,\mathrm{d}\mathbf{r}\times\mathbf{B}=\vec{0}</math></center> | \mathrm{d}\mathbf{F}_m=\int_{\Gamma}\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\!\vee I\,\mathrm{d}\mathbf{r}\times\mathbf{B}=\vec{0}</math></center> | ||
Revisión de 18:49 28 abr 2013
1 Enunciado
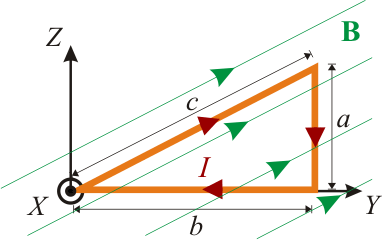
Una espira de corriente que transporta una corriente de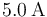 tiene forma de triángulo rectángulo con lados
tiene forma de triángulo rectángulo con lados 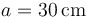 ,
, 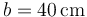 y
y 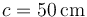 . Se sitúa la espira en una región donde existe un campo magnético uniforme de magnitud
. Se sitúa la espira en una región donde existe un campo magnético uniforme de magnitud 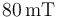 y cuya dirección es paralela al lado c. Calcular:
y cuya dirección es paralela al lado c. Calcular:
- Fuerza ejercida por el campo magnético sobre cada lado de la espira.
- Momento dipolar magnético de la espira.
- Módulo del par ejercido por el campo magnético sobre la espira de corriente.
2 Solución
Tomamos un sistema de referencia cartesiano tal que la espira Γ de vértices A, B y C, están contenida en un plano paralelo al OYZ, con los catetos 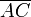 y
y 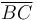 dispuestos paralelamente a los ejes OY y OZ, respectivamente. La espira está sometida a un campo magnético uniforme (constante en todos los puntos del espacio), paralelo a la hipotenusa
dispuestos paralelamente a los ejes OY y OZ, respectivamente. La espira está sometida a un campo magnético uniforme (constante en todos los puntos del espacio), paralelo a la hipotenusa  , y de módulo conocido:
, y de módulo conocido:
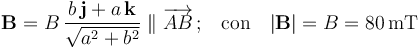
Cuando la espira es recorrida por una intensidad de corriente 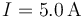 , sobre los elementos de corriente
, sobre los elementos de corriente 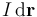 definidos en cada uno de sus puntos, se ejercen fuerzas infinitesimales que, al sumarlas todas, producen una resultante nula:
definidos en cada uno de sus puntos, se ejercen fuerzas infinitesimales que, al sumarlas todas, producen una resultante nula: