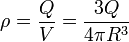Principios de la electrostática (GIE)

De Laplace

(Diferencias entre revisiones)

Revisión de 17:32 22 abr 2013

Contenido

1 Concepto de electrostática
2 Ley de Coulomb
3 Principio de superposición
4 Campo eléctrico
5 Líneas de campo eléctrico
6 Campo de una distribución de carga

1 Concepto de electrostática

La Electrostática es la parte del electromagnetismo que estudia la interacción entre cargas eléctricas en reposo.

Por estar cargadas y a una cierta distancia, las partículas ejercen fuerzas eléctricas unas sobre otras. De acuerdo con la segunda Ley de Newton, el resultado de estas fuerzas debe ser un movimiento acelerado de las diferentes cargas. Supondremos que esto no ocurre porque actúan sobre ellas otras fuerzas no consideradas que retienen a las cargas en la misma posición.

A pesar de su aparente irrealidad (ya que una carga no puede mantenerse inmóvil flotando en el espacio), la electrostática posee una gran aplicación ya que no solo describe aproximadamente situaciones reales, sino porque sirve de fundamento para otras situaciones electromagnéticas. En el campo de la electrostática aparecen el principio de superposición, la ley de Gauss, el potencial eléctrico, la ecuación de Laplace… todos los cuales se utilizan más adelante.

La electrostática se subdivide en dos situaciones:

Electrostática en el vacío: Supone que las cargas están inmóviles flotando en el espacio.

Electrostática en medios materiales: Supone que las cargas se encuentran en el interior o en la superficie de medios materiales. A su vez, éstos se suelen clasificar en dos tipos:

Conductores: Son aquellos materiales (típicamente metálicos) que permiten el movimiento de cargas por su interior. En electrostática esto implica que las cargas se encuentran en equilibrio ya que pudiendo moverse no lo hacen.
Dieléctricos: Son aquellos materiales (típicamente plásticos) que no permiten el movimiento de cargas por su interior. En electrostática esto implica la existencia de cargas ligadas, que no pueden abandonar los átomos a los que pertenecen.

Aunque en la mayoría de los casos prácticos consideraremos cargas dentro de medios materiales, la electrostática en el vacío es válida como fundamento de todo lo que sigue, puesto que estos son vacío en su mayor parte.

2 Ley de Coulomb

La ley de Coulomb fue descubierta por Henry Cavendish, que no lo publicó. Varios años después, Coulomb redescubrió esta ley, publicándolo adecuadamente, por lo que recibe su nombre.

Es una ley física que nos describe la fuerza entre dos cargas puntuales en reposo. Nos dice que si tenemos dos cargas puntuales $q 1$ y $q 2$ situadas a una distancia $d 12$ , aparece una fuerza eléctrica entre ellas tal que:

Módulo

es proporcional al producto de las cargas.
es inversamente proporcional al cuadrado de la distancia entre las cargas.

Dirección

Es la de la recta que pasa por las dos cargas

Sentido

Depende del signo de las cargas

Cargas del mismo signo se repelen
Cargas de distinto signo se atraen

Matemáticamente esto se expresa como que la fuerza que produce la carga 1 sobre la 2 es

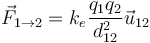
$\vec{F}_{1\to 2} = k_e \frac{q_1 q_2}{d_{12}^2}\vec{u}_{12}$

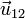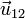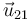siendo $\vec{u}_{12}$ el vector unitario en la dirección de la recta que pasa por las dos cargas y lleva el sentido de la 1 a la 2, es decir, hacia fuera de las dos cargas. La fuerza que la 2 produce sobre la 1 se calculará del mismo modo, sustituyendo $\vec{u}_{12}$ por $\vec{u}_{21}$ que es el unitario opuesto.

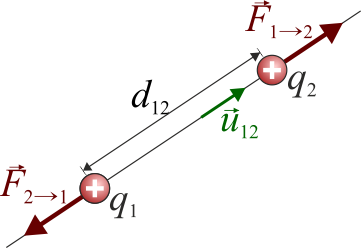
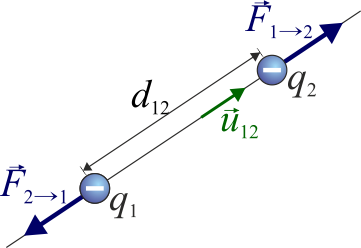
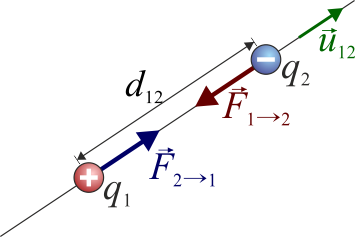
Esta expresión es válida tanto si las cargas son del mismo signo como si son de signos opuestos. En el segundo caso, el producto de las cargas es negativo y resulta una fuerza atractiva.

La constante $k e$ universal que, por la forma en que se eligen las unidades en el SI tiene un valor exacto

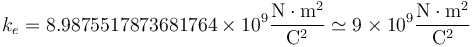
$k_e = 8.9875517873681764\times 10^9\frac{\mathrm{N}\cdot\mathrm{m}^2}{\mathrm{C}^2}\simeq 9\times 10^{9}\frac{\mathrm{N}\cdot\mathrm{m}^2}{\mathrm{C}^2}$

siendo el segundo valor mucho más fácil de recorrar y con un error de solo el 0.1%.

Esta constante de proporcionalidad suele escribirse en la forma aparentemente más complicada

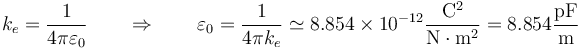
$k_e = \frac{1}{4\pi\varepsilon_0}\qquad\Rightarrow\qquad \varepsilon_0 = \frac{1}{4\pi k_e} \simeq 8.854\times 10^{-12}\frac{\mathrm{C}^2}{\mathrm{N}\cdot\mathrm{m}^2}=8.854\frac{\mathrm{pF}}{\mathrm{m}}$

La razón de escribirlo de esta forma se halla en la ley de Gauss.

Si lo que conocemos son los vectores de posición de las dos cargas respecto a un sistema de referencia, podemos escribir la ley de Coulomb en función de estos vectores, ya que

$d_{12}=\left|\vec{r}_2-\vec{r}_1\right|\qquad\qquad \vec{u}_{12}=\frac{\vec{r}_2-\vec{r}_1}{\left|\vec{r}_2-\vec{r}_1\right|}$

y queda

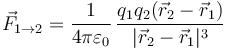
$\vec{F}_{1\to 2} = \frac{1}{4\pi\varepsilon_0}\,\frac{q_1q_2(\vec{r}_2-\vec{r}_1)}{|\vec{r}_2-\vec{r}_1|^3}$

Hay que destacar (porque es fuente de errores) el cambio del exponente del denominador de 2 a 3, al introducir una distancia más en la normalización del vector de posición relativo.

Como ilustración de la magnitud la fuerza eléctrica podemos considerar la atracción entre un protón y un electrón que se hallan a una distancia de un radio de Bohr (tamaño del átomo de hidrógeno)

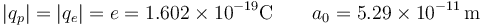
$|q_p| = |q_e| = e = 1.602\times 10^{-19}\mathrm{C}\qquad a_0 =5.29\times 10^{-11}\,\mathrm{m}$

Resulta un módulo de la fuerza

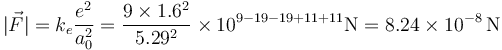
$|\vec{F}| = k_e\frac{e^2}{a_0^2} = \frac{9\times 1.6^2}{5.29^2}\times 10^{9-19-19+11+11}\mathrm{N} = 8.24\times 10^{-8}\,\mathrm{N}$

Esta fuerza no parece excesivamente intensa, pero debemos tener en cuenta que actúa sobre un electrón, cuya masa es minúscula. La aceleración que produce esta fuerza es

$|\vec{a}| = \frac{|\vec{F}|}{m} = \frac{8.24\times 10^{-8}}{9.1\times 10^{-31}\mathrm{kg}}=9.04\times 10^{22}\frac{\mathrm{m}}{\mathrm{s}^2} = 9.22\times 10^{21}g$

Dicho de otra forma, la fuerza debida a un solo protón es 9000000000000000000000 veces la atracción gravitatoria debida a la Tierra entera.

Otra comparación posible es la de la fuerza eléctrica entre el protón y el electrón y la fuerza gravitatoria entre ellas. Su cociente vale

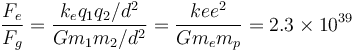
$\frac{F_e}{F_g}=\frac{k_e q_1q_2/d^2}{G m_1 m_2/d^2}=\frac{ke e^2}{G m_em_p} = 2.3\times 10^{39}$

es decir, la fuerza eléctrica es 2300000000000000000000000000000000000000 veces más intensa que la gravitatoria.

3 Principio de superposición

La ley de Coulomb nos da la fuerza entre dos cargas puntuales, pero no nos dice nada de qué ocurre si tenemos más de dos cargas o estas no son puntuales.

Por ejemplo, supongamos que tenemos tres cargas alineadas y queremos hallar la fuerza sobre una de las cargas de los extremos. ¿Cómo influye la presencia de la carga central? ¿Impide que las cargas de los extremos se “vean”, apantallándolas, o, por el contrario, no afecta a la fuerza entre ellas?

La evidencia es que ocurre lo segundo, lo que se puede expresar mediante el denominado principio de superposición:

Dado un sistema de cargas puntuales, la fuerza eléctrica sobre cada una de ellas es la suma vectorial de las fuerzas debidas a cada una de las demás cargas, como si el resto de cargas no estuvieran presentes.

La última parte del enunciado es crucial. Es natural que la fuerza sobre una carga sea la suma de diferentes contribuciones, cada una debida a una carga diferente. Lo que es novedoso es que para calcular esa contribución podemos ignorar por completo la existencia del resto de cargas, es decir, podemos calcular cada término mediante la ley de Coulomb.

Así, si tenemos tres cargas, $q 1$ , $q 2$ y $q 3$ . La fuerza sobre la carga 1 será

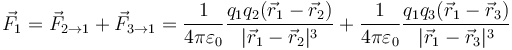
$\vec{F}_1 = \vec{F}_{2\to 1} + \vec{F}_{3\to 1} = \frac{1}{4\pi\varepsilon_0}\frac{q_1q_2(\vec{r}_1-\vec{r}_2)}{|\vec{r}_1-\vec{r}_2|^3}+ \frac{1}{4\pi\varepsilon_0}\frac{q_1q_3(\vec{r}_1-\vec{r}_3)}{|\vec{r}_1-\vec{r}_3|^3}$

Más en general, si tenemos un sistema de N cargas actuando sobre una carga $q 0$ , la fuerza sobre esta vendrá dada por la suma

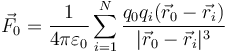
$\vec{F}_0 = \frac{1}{4\pi\varepsilon_0}\sum_{i=1}^N \frac{q_0q_i(\vec{r}_0-\vec{r}_i)}{|\vec{r}_0-\vec{r}_i|^3}$

Es importante no confundir el principio de superposición de fuerzas electrostáticas con la resultante sobre un sistema de partículas. El principio de superposición nos da la fuerza sobre una sola carga, pero si queremos hallar la fuerza sobre un conjunto de cargas (un sólido con miles de cargas, por ejemplo), habrá que calcular la resultante y, si es preciso, el momento de las fuerzas.

4 Campo eléctrico

4.1 Definición

La expresión de la fuerza sobre una carga puntual debida a un sistema de N cargas puede factorizarse también en la forma

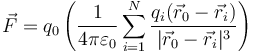
$\vec{F} = q_0\left(\frac{1}{4\pi\varepsilon_0}\sum_{i=1}^N \frac{q_i(\vec{r}_0-\vec{r}_i)}{|\vec{r}_0-\vec{r}_i|^3}\right)$

y reescribirse como el producto

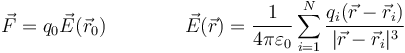
$\vec{F}=q_0\vec{E}(\vec{r}_0)\qquad\qquad \vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\sum_{i=1}^N \frac{q_i(\vec{r}-\vec{r}_i)}{|\vec{r}-\vec{r}_i|^3}$

siendo 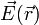$\vec{E}(\vec{r})$ el campo eléctrico debido a las N cargas. Si examinamos la expresión vemos que en el campo eléctrico no aparece ninguna propiedad de la carga que experimenta la fuerza, ni su magnitud $q 0$ , ni su posición 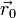$\vec{r}_0$ . El campo eléctrico es consecuencia exclusivamente de la distribución de N cargas.

Matemáticamente, se trata de un campo vectorial que a cada punto del espacio $\vec{r}$ le asigna un vector 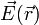$\vec{E}(\vec{r})$ .

Físicamente entendemos el campo electrostático como una perturbación en el espacio producida por la presencia de cargas eléctricas en reposo

El campo es un concepto primario. No se puede describir qué es el campo eléctrico, sino solo qué efectos produce sobre otras cargas.

Aunque hemos introducido el campo eléctrico a partir de un sumatorio, no es así como se define, ya que en general ni conocemos cuántas cargas tenemos ni dónde se encuentra cada una. Puede definirse de una manera operativa, esto es, dando un procedimiento para su medida. Para ello se considera una carga muy pequeña $q 0$ y se sitúa en un campo eléctrico. Con la medida de un dinamómetro se mide la fuerza sobre ella. Se define el campo eléctrico en la posición de la carga como

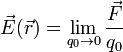
$\vec{E}(\vec{r})=\lim_{q_0\to 0}\frac{\vec{F}}{q_0}$

El límite se toma porque idealmente se considera que la carga que se coloca no debe afectar a lo que ya había, para lo cual debe ser lo más pequeña posible.

4.2 Campo de una carga puntual

Particularizando el sumatorio, si tenemos una sola carga puntual situada en el origen de coordenadas (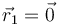 $\vec{r}_1=\vec{0}$ ) el campo eléctrico producido por ella será

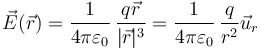
$\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\,\frac{q\vec{r}}{|\vec{r}|^3}=\frac{1}{4\pi\varepsilon_0}\,\frac{q}{r^2}\vec{u}_r$

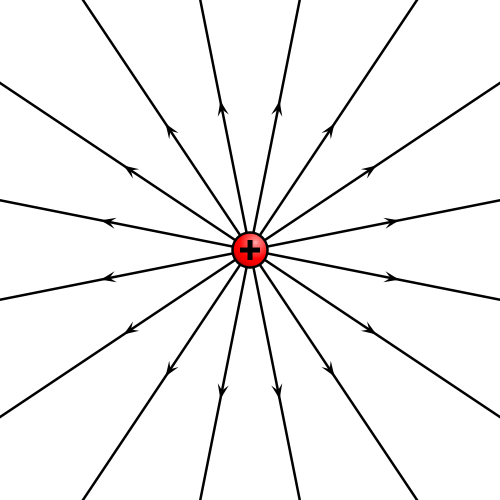
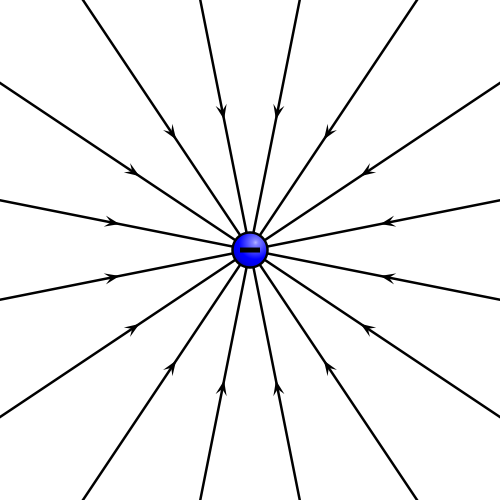
Este campo es radial desde la carga. Va hacia afuera si esta es positiva (se dice que tenemos un manantial de campo) y hacia adentro si es negativa (tenemos un sumidero). El campo decae como el cuadrado de la distancia. A doble distancia, cuarta parte de campo.

(ilustraciones obra de Geek3 para Wikipedia).

4.3 Reinterpretación de la ley de Coulomb

Una vez que tenemos el campo eléctrico creado por una carga puntual podemos reinterpretar la ley de Coulomb.

Tal como la formularon Cavendish y Coulomb, la fuerza entre cargas es una ley de acción a distancia. Tenemos dos cargas separadas y cada una percibe la presencia de la otra.

En términos del campo eléctrico, la fuerza la da una ley local. Una carga, positiva o negativa, por el hecho de existir crea una perturbación en el espacio que denominamos campo eléctrico. La segunda carga lo que percibe es el campo de la primera en el punto en que se encuentra, pero no “sabe” quién crea ese campo, si una carga puntual, o una esfera cargada, por ejemplo.

Matemáticamente, si tenemos una carga $q 1$ en 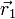$\vec{r}_1$ y situamos una carga $q 2$ en el punto 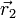$\vec{r}_2$ , la fuerza que experimenta es el producto de la carga por el campo en la posición que se encuentra

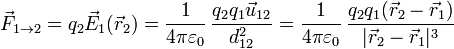
$\vec{F}_{1\to 2}= q_2\vec{E}_1(\vec{r}_2) = \frac{1}{4\pi\varepsilon_0}\,\frac{q_2q_1\vec{u}_{12}}{d_{12}^2} = \frac{1}{4\pi\varepsilon_0}\,\frac{q_2q_1(\vec{r}_2-\vec{r}_1)}{|\vec{r}_2-\vec{r}_1|^3}$

siendo 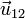$\vec{u}_{12}$ el vector unitario en la dirección de la recta que pasa por las dos cargas y en el sentido de la carga 1 a la 2. Esta es la conocida como ley de Coulomb para fuerzas entre cargas puntuales.

Dado que la fuerza es proporcional a la carga $q 2$ , si tenemos una carga $q 1$ positiva, la fuerza sobre $q 2$ será de repulsión si $q 2$ es positiva y de atracción si es negativa, aunque en los dos casos el campo de $q 1$ vaya hacia afuera.

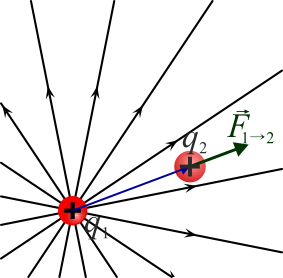
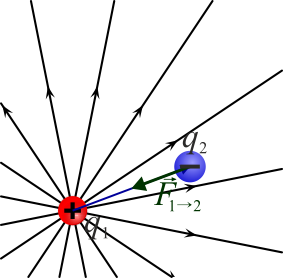
La fuerza que experimenta la carga 1 se debe a que percibe el campo de la carga 2

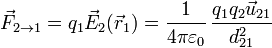
$\vec{F}_{2\to 1}= q_1\vec{E}_2(\vec{r}_1) = \frac{1}{4\pi\varepsilon_0}\,\frac{q_1q_2\vec{u}_{21}}{d_{21}^2}$

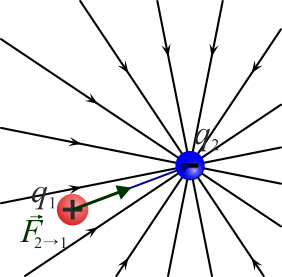
Puesto que el producto de cargas es conmutativo, la distancia es la misma en los dos casos y el vector unitario tiene la misma dirección, pero sentido opuesto al anterior, se llega a que la ley de Coulomb cumple la tercera ley de Newton

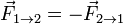
$\vec{F}_{1\to 2} = -\vec{F}_{2\to 1}$

5 Líneas de campo eléctrico

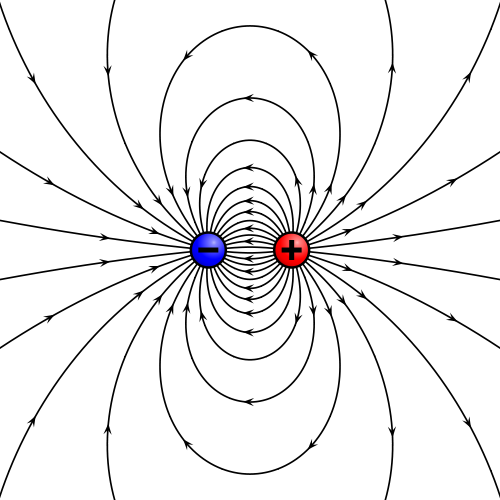
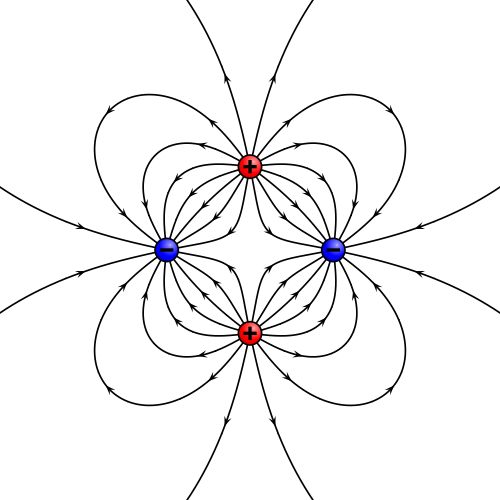
Como con cualquier otro campo, se pueden trazar las líneas de campo eléctrico, como aquellas curvas que son tangentes al campo eléctrico en cada punto. Estas curvas son soluciones de la ecuación diferencial

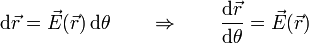
$\mathrm{d}\vec{r}=\vec{E}(\vec{r})\,\mathrm{d}\theta\qquad\Rightarrow\qquad \frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}=\vec{E}(\vec{r})$

siendo $θ$ un parámetro que nos permite etiquetar los puntos de cada curva. Estas ecuaciones diferenciales suelen ser extremadamente complejas y no poseen soluciones analíticas salvo en los casos más triviales, por lo que su solución requiere el uso de ordenadores, como en el caso de las cuatro cargas representado más arriba.

Existe casos particulares importantes:

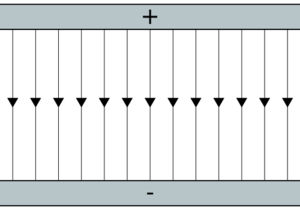
Un campo uniforme (independiente de la posición) tiene líneas de campo que son rectas paralelas. Este es el caso del campo eléctrico en el interior de un condensador plano.

Un campo central

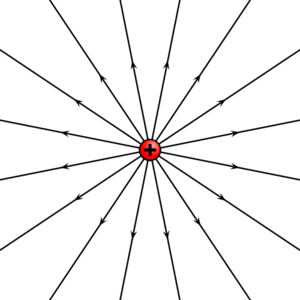
$\vec{E}(\vec{r}) = E(r)\vec{u}_r\qquad \qquad (\mbox{campo central})$

en el cual el campo es siempre puramente radial, las líneas de campo son semirrectas radiales. Este es el caso del campo de una carga puntual, positiva o negativa,

6 Campo de una distribución de carga

6.1 De cargas puntuales

El principio de superposición se extiende a cualquier número de cargas. Si tenemos N cargas puntuales, situadas en los puntos 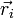$\vec{r}_i$ , el campo en cualquier punto vale

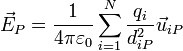
$\vec{E}_P=\frac{1}{4\pi\varepsilon_0}\sum_{i=1}^N \frac{q_i}{d_{iP}^2}\vec{u}_{iP}$

o, usando las posiciones de cada una

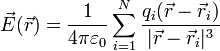
$\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\sum_{i=1}^N \frac{q_i(\vec{r}-\vec{r}_i)}{|\vec{r}-\vec{r}_i|^3}$

6.2 De una distribución continua

Al considerar un medio material, se hace imposible conocer la posición de cada una de los trillones de cargas que lo componen.

Por ello, se debe trabajar con densidades de carga. Dividimos el volumen del material en elementos microscópicos (pero que contienen millones de cargas), de forma que la carga de cada elemento es $d q$ . Entonces, el campo en un punto P es la generalización de la suma anterior a una integral

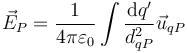
$\vec{E}_P = \frac{1}{4\pi\varepsilon_0}\int \frac{\mathrm{d}q'}{d_{qP}^2}\vec{u}_{qP}$

siendo $d q P$ la distancia desde cada elemento de carga al punto donde queremos hallar el campo y 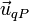$\vec{u}_{qP}$ el unitario en la dirección desde el elemento de carga al punto en cuestión.

Esta expresión se puede escribir empleando las posiciones de las cargas. Si designamos por $\vec{r}$ la posición del punto donde deseamos hallar el campo eléctrico y por 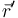$\vec{r}'$ la posición de un elemento de carga ('ojo con la prima '!) queda

$d_{qP}=|\vec{r}-\vec{r}'|\qquad\qquad \vec{u}_{qP}=\frac{\vec{r}-\vec{r}'}{|\vec{r}-\vec{r}'|}$

y queda la integral

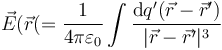
$\vec{E}(\vec{r}(=\frac{1}{4\pi\varepsilon_0}\int \frac{\mathrm{d}q'(\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3}$

Dependiendo del tipo de distribución de carga que tengamos, el tipo de integral variará.

Volumétrica: Si la carga está repartida en un volumen

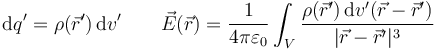
$\mathrm{d}q'=\rho(\vec{r}')\,\mathrm{d}v'\qquad \vec{E}(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\int_V \frac{\rho(\vec{r}')\,\mathrm{d}v'(\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3}$

donde

ρ

será en general una función de la posición 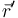$\vec{r}'$ , que habrá que integrar.

Superficial: Si la carga está distribuida sobre una superficie

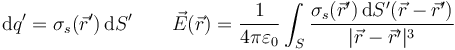
$\mathrm{d}q'=\sigma_s(\vec{r}')\,\mathrm{d}S'\qquad \vec{E}(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\int_S \frac{\sigma_s(\vec{r}')\,\mathrm{d}S'(\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3}$

Obsérvese que, a diferencia del flujo, aquí el diferencial de superficie es escalar, e igual al área del elemento.

Lineal: Si la carga está repartida a lo largo de una línea

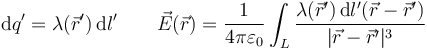
$\mathrm{d}q'=\lambda(\vec{r}')\,\mathrm{d}l'\qquad \vec{E}(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\int_L \frac{\lambda(\vec{r}')\,\mathrm{d}l'(\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3}$

Caso general: En un problema general podemos tener todos los tipos de densidades simultáneamente y además cargas puntuales aisladas. El campo en cada punto será la superposición de los campos individuales

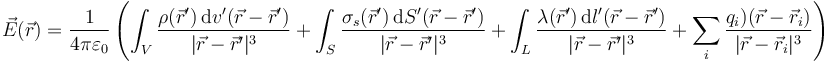
$\vec{E}(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\left(\int_V \frac{\rho(\vec{r}')\,\mathrm{d}v'(\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3}+\int_S \frac{\sigma_s(\vec{r}')\,\mathrm{d}S'(\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3}+\int_L \frac{\lambda(\vec{r}')\,\mathrm{d}l'(\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3}+\sum_i \frac{q_i)(\vec{r}-\vec{r}_i)}{|\vec{r}-\vec{r}_i|^3}\right)$

En casi todos los casos estas integrales son imposibles de hallar analíticamente. Sin embargo, se prestan a un cálculo numérico sencillo de implementar en un ordenador: se divide la distribución en un número grande de elementos, se calcula la contribución de cada uno al campo y se halla la suma de todos ellos, como si fuera un conjunto de cargas puntuales. Existen diferentes mejoras a este método, que aumentan la precisión o la velocidad del cálculo.

6.3 Densidades uniformes

En muchos problemas prácticos se dice “una carga Q distribuida uniformemente en el volumen” o “un anillo cargado uniformemente con carga Q” o similar. En estos casos se nos está dando el tipo de distribución (si es de volumen, lineal, etc.), el valor de la carga total, y se nos dice que la carga tiene una densidad uniforme, es decir, que es la misma para todos los puntos. En esos casos, lo primero es determinar la densidad correspondiente, y luego recurrir a las expresiones anteriores.

Por ejemplo, si se nos pide hallar el campo en los puntos del eje de un anillo de radio $R$ con una carga $Q$ distribuida uniformemente, tenemos que el anillo tiene una densidad lineal de carga $λ$ , tal que

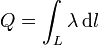
$Q = \int_L \lambda\,\mathrm{d}l$

Ahora bien, por ser la densidad uniforme, puede salir de la integral

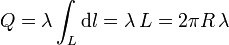
$Q = \lambda\int_L\mathrm{d}l = \lambda\,L = 2\pi R\,\lambda$

lo que nos da la densidad

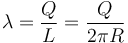
$\lambda = \frac{Q}{L}=\frac{Q}{2\pi R}$

y, para la expresión del campo nos queda

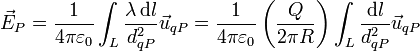
$\vec{E}_P = \frac{1}{4\pi\varepsilon_0}\int_L \frac{\lambda\,\mathrm{d}l}{d_{qP}^2}\vec{u}_{qP}=\frac{1}{4\pi\varepsilon_0}\left(\frac{Q}{2\pi R}\right)\int_L \frac{\mathrm{d}l}{d_{qP}^2}\vec{u}_{qP}$

Análogamente si tenemos el caso de una carga distribuida uniformemente en una superficie esférica

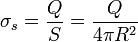
$\sigma_s = \frac{Q}{S}=\frac{Q}{4\pi R^2}$

o en un volumen esférico

$\rho = \frac{Q}{V}=\frac{3Q}{4\pi R^3}$

@@ Línea 243: / Línea 243: @@
 * Caso general: En un problema general podemos tener todos los tipos de densidades simultáneamente y además cargas puntuales aisladas. El campo en cada punto será la superposición de los campos individuales
-<center><math>\vec{E}(\vec{r}) = </math></center>
+<center><math>\vec{E}(\vec{r}) = \frac{1}{4\pi\varepsilon_0}\left(\int_V \frac{\rho(\vec{r}')\,\mathrm{d}v'(\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3}+\int_S \frac{\sigma_s(\vec{r}')\,\mathrm{d}S'(\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3}+\int_L \frac{\lambda(\vec{r}')\,\mathrm{d}l'(\vec{r}-\vec{r}')}{|\vec{r}-\vec{r}'|^3}+\sum_i \frac{q_i)(\vec{r}-\vec{r}_i)}{|\vec{r}-\vec{r}_i|^3}\right)</math></center>
 [[Archivo:Campo-anillo-suma-01.jpg|right]]En casi todos los casos estas integrales son imposibles de hallar analíticamente. Sin embargo, se prestan a un cálculo numérico sencillo de implementar en un ordenador: se divide la distribución en un número grande de elementos, se calcula la contribución de cada uno al campo y se halla la suma de todos ellos, como si fuera un conjunto de cargas puntuales. Existen diferentes mejoras a este método, que aumentan la precisión o la velocidad del cálculo.

Principios de la electrostática (GIE)

De Laplace

Revisión de 17:32 22 abr 2013

Contenido

1 Concepto de electrostática

2 Ley de Coulomb

3 Principio de superposición

4 Campo eléctrico

4.1 Definición

4.2 Campo de una carga puntual

4.3 Reinterpretación de la ley de Coulomb

5 Líneas de campo eléctrico

6 Campo de una distribución de carga

6.1 De cargas puntuales

6.2 De una distribución continua

6.3 Densidades uniformes

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES