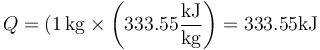Trabajo en fusión de hielo
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Tenemos 1 kg de hielo (densidad de masa 917 kg/m³) a 0 °C, al cual se le cede lentamente calor a una presión de 101.3 kPa has…') |
|||
| Línea 7: | Línea 7: | ||
==Calor== | ==Calor== | ||
| + | A presión constante, el calor es proporcional a la masa que se derrite | ||
| + | |||
| + | <center><math>Q=m\,\Delta h_f</math></center> | ||
| + | |||
| + | siendo <center><math>\Delta h_f</math></center> la entalpía específica de fusión (o calor latente de fusión), cuyo valor para la fusión del hielo a 1 atm es | ||
| + | |||
| + | <center><math>\Delta h_f = L_f = 333.55\,\frac{\mathrm{kJ}}{\mathrm{kg}}</math></center> | ||
| + | |||
| + | por lo que, siendo la masa 1 kg el calor que entra en el sistema es simplemente | ||
| + | |||
| + | <center><math>Q = (1\,\mathrm{kg}\times\left(333.55\frac{\mathrm{kJ}}{\mathrm{kg}}\right)=333.55\mathrm{kJ}</math></center> | ||
==Trabajo== | ==Trabajo== | ||
==Entalpía y energía interna== | ==Entalpía y energía interna== | ||
Revisión de 16:09 22 feb 2013
Contenido |
1 Enunciado
Tenemos 1 kg de hielo (densidad de masa 917 kg/m³) a 0 °C, al cual se le cede lentamente calor a una presión de 101.3 kPa hasta que convierte por completo en agua (densidad de masa 1000 kg/m³). Para este proceso, halle
- El calor que entra en el sistema
- El trabajo realizado sobre el sistema
- La variación de entalpía y de energía interna del sistema
2 Calor
A presión constante, el calor es proporcional a la masa que se derrite


por lo que, siendo la masa 1 kg el calor que entra en el sistema es simplemente