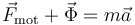Entrar Página Discusión Historial Go to the site toolbox

3.13. Partícula motorizada en aro (Ex.Ene/13)

De Laplace

(Diferencias entre revisiones)
(→Trabajo realizado por el motor sobre la partícula)
(→Trabajo realizado por el motor sobre la partícula)
Línea 44: Línea 44:
P_W=\frac{dW}{dt}=\vec{F}_{\mathrm{mot}}\cdot\vec{v}=ma_t\vec{T}\cdot R\omega\vec{T}=ma_tR\omega
P_W=\frac{dW}{dt}=\vec{F}_{\mathrm{mot}}\cdot\vec{v}=ma_t\vec{T}\cdot R\omega\vec{T}=ma_tR\omega
</math></center>
</math></center>
-
De aquí despejar el trabajo infinitesimal:
+
De aquí, despejar el trabajo infinitesimal:
<center><math>
<center><math>
-
dW=ma_tR\,\omega dt=ma_tRd\theta=\frac{1}{2}KmR^2d\theta
+
dW=ma_tR\,\omega dt=ma_tR\,d\theta=\frac{1}{2}KmR^2d\theta
</math></center>
</math></center>
Y, por último, integrar entre <math>\theta=0\,</math> y <math>\theta=\pi/2\,\mathrm{rad}\,</math>
Y, por último, integrar entre <math>\theta=0\,</math> y <math>\theta=\pi/2\,\mathrm{rad}\,</math>

Revisión de 15:33 20 feb 2013

Contenido

1 Enunciado

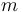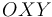Una partícula P\,, de masa m\,, está ensartada sin rozamiento en un aro fijo de radio R\,, el cual se halla situado en el plano horizontal OXY\, y tiene su centro en el origen de coordenadas O\,. Un motor ejerce una fuerza tangencial sobre la partícula, y como resultado ésta se mueve en sentido antihorario con una velocidad angular (escalar) que es función de la posición:

\omega=\sqrt{K\theta} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(\theta\geq 0)

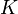donde K\, es una constante positiva conocida, y el ángulo \theta\, (definido en la figura) es el parámetro utilizado para describir la posición de la partícula sobre el aro.

  1. Determine la aceleración angular en función de la posición. ¿Qué tipo de movimiento circular realiza la partícula?
  2. Halle las componentes intrínsecas de la aceleración lineal en función de la posición.
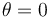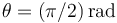  3. Calcule el trabajo que realiza el motor sobre la partícula al moverse ésta desde \theta=0\, hasta \theta=(\pi/2)\,\mathrm{rad}\,.
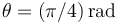  4. Determine la fuerza de reacción vincular ejercida por el aro sobre la partícula para la posición \theta=(\pi/4)\,\mathrm{rad}\,.

2 Aceleración angular y tipo de movimiento circular

Hallamos la aceleración angular (escalar) como la derivada respecto al tiempo de la velocidad angular (escalar):

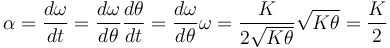
\alpha = \frac{d\omega}{dt} = \frac{d\omega}{d\theta}\frac{d\theta}{dt}=\frac{d\omega}{d\theta}\omega=\frac{K}{2\sqrt{K\theta}}\sqrt{K\theta}=\frac{K}{2}

Se observa que la aceleración angular (escalar) obtenida es una constante en el tiempo (no depende de la posición de la partícula). Por tanto, la partícula realiza un movimiento circular uniformemente acelerado.

Para expresar la aceleración angular en forma vectorial, tendremos en cuenta que en un movimiento circular la velocidad angular y la aceleración angular son paralelas entre sí y perpendiculares al plano de giro. 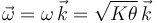Además, como se nos indica en el enunciado que la partícula se mueve en sentido antihorario, sabemos que el vector velocidad angular apunta en el sentido positivo del eje OZ\,, es decir: \vec{\omega}=\omega\,\vec{k}=\sqrt{K\theta}\,\vec{k}\,. Y entonces la aceleración angular:

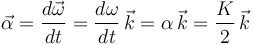
\vec{\alpha} = \frac{d\vec{\omega}}{dt}= \frac{d\omega}{dt}\,\vec{k}=\alpha\,\vec{k} = \frac{K}{2}\,\vec{k}

3 Componentes intrínsecas de la aceleración

Tratándose de un movimiento circular (estudiado de forma específica en el tema), podemos aplicar directamente las expresiones deducidas en la teoría para las componentes intrínsecas de la aceleración en este tipo de movimiento:

a_t=R\alpha=\frac{RK}{2}\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, a_n=R\omega^2=RK\theta

Observamos que la aceleración tangencial es constante (movimiento uniformemente acelerado), mientras que la aceleración normal sí que depende de la posición (crece linealmente con \theta\,).

4 Trabajo realizado por el motor sobre la partícula

Sobre la partícula actúan dos fuerzas: la que ejerce el motor (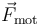\vec{F}_{\mathrm{mot}}\,) y la de reacción vincular (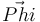\vec{Phi}\,) ejercida por el aro. Pero sólo realiza trabajo sobre la partícula la fuerza motora (que es tangencial, según se nos indica en el enunciado). La fuerza de reacción vincular (f.r.v.) no trabaja porque, al ser el aro un vínculo liso (sin rozamiento) y esclerónomo (fijo), sabemos que la f.r.v. es perpendicular en todo instante al desplazamiento de la partícula.

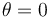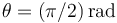En consecuencia, calcular el trabajo que realiza el motor sobre la partícula al moverse ésta desde \theta=0\, hasta \theta=(\pi/2)\,\mathrm{rad}\, es equivalente a calcular el trabajo total desarrollado sobre la partícula en ese fragmento de trayectoria. Podemos, pues, aplicar el teorema de la energía o teorema de las fuerzas vivas, que nos dice que el trabajo total desarrollado sobre la partícula es igual a la variación que experimenta su energía cinética:

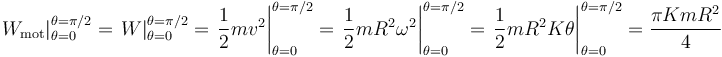
\left.W_{\mathrm{mot}}\right|_{\theta=0}^{\theta=\pi/2}=\left.W\right|_{\theta=0}^{\theta=\pi/2}=\left.\frac{1}{2}mv^2\right|_{\theta=0}^{\theta=\pi/2}=\left.\frac{1}{2}mR^2\omega^2\right|_{\theta=0}^{\theta=\pi/2}=\left.\frac{1}{2}mR^2K\theta\right|_{\theta=0}^{\theta=\pi/2}=\frac{\pi KmR^2}{4}

Un procedimiento alternativo para el cálculo de este trabajo consiste en determinar primero la potencia mecánica desarrollada sobre la partícula:

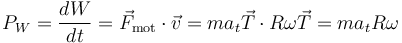
P_W=\frac{dW}{dt}=\vec{F}_{\mathrm{mot}}\cdot\vec{v}=ma_t\vec{T}\cdot R\omega\vec{T}=ma_tR\omega

De aquí, despejar el trabajo infinitesimal:

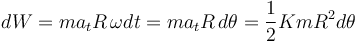
dW=ma_tR\,\omega dt=ma_tR\,d\theta=\frac{1}{2}KmR^2d\theta

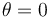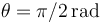
Y, por último, integrar entre \theta=0\, y \theta=\pi/2\,\mathrm{rad}\,

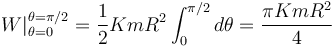
\left.W\right|_{\theta=0}^{\theta=\pi/2}=\frac{1}{2}KmR^2\int_{0}^{\pi/2}d\theta=\frac{\pi KmR^2}{4}

5 Fuerza de reacción vincular

Conforme a la segunda ley de Newton, la suma de las fuerzas que actúan sobre la partícula es igual a masa por aceleración:

\vec{F}_{\mathrm{mot}}+\vec{\Phi}=m\vec{a}
Obtenido de "http://tesla.us.es/wiki/index.php/3.13._Part%C3%ADcula_motorizada_en_aro_(Ex.Ene/13)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace