Propiedades de un sistema de tres partículas
De Laplace
(→Cantidad de movimiento) |
(→Cantidad de movimiento) |
||
| Línea 30: | Línea 30: | ||
<center><math>\vec{p}=\left(100(-10\vec{\jmath})+200(-10\vec{\imath})+100(10\vec{\jmath})\right)\frac{\mathrm{g}\cdot\mathrm{cm}}{\mathrm{s}}=\left(-2000\vec{\imath}\right)\frac{\mathrm{g}\cdot\mathrm{cm}}{\mathrm{s}}=\left(-0.02\vec{\imath}\right)\frac{\mathrm{kg}\cdot\mathrm{m}}{\mathrm{s}}</math></center> | <center><math>\vec{p}=\left(100(-10\vec{\jmath})+200(-10\vec{\imath})+100(10\vec{\jmath})\right)\frac{\mathrm{g}\cdot\mathrm{cm}}{\mathrm{s}}=\left(-2000\vec{\imath}\right)\frac{\mathrm{g}\cdot\mathrm{cm}}{\mathrm{s}}=\left(-0.02\vec{\imath}\right)\frac{\mathrm{kg}\cdot\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | A partir de la cantidad de movimiento podemos hallar la velocidad del CM dividiendo por la masa total | ||
| + | |||
| + | \vec{v}_C = \frac{\vec{p}{M}=\left(\frac{-2000\vec{\imath}}{400}\right)\frac{\mathrm{cm}}{\mathrm{s}}= \left(-5\vec{\imath}\right)\frac{\mathrm{cm}}{\mathrm{s}} | ||
==Momento cinético== | ==Momento cinético== | ||
Revisión de 19:32 26 ene 2013
Contenido |
1 Enunciado
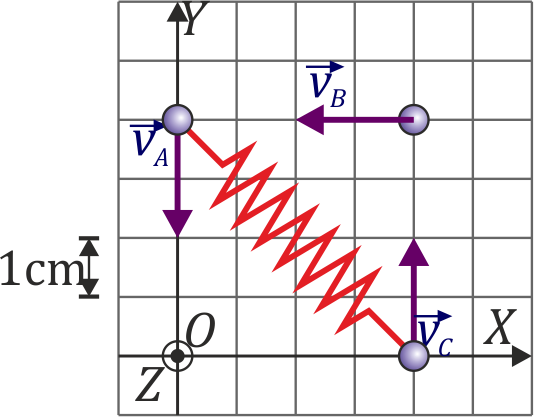
Considere un sistema de tres partículas de masas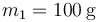 
, 
, 
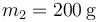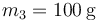que en un instante dado están situadas en las posiciones de la figura y moviéndose con la velocidad indicada, siendo la rapidez de cada una de ellas 
. Suponga
que la masa 1 y la 3 está unidas por un resorte de longitud natural nula y constante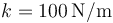 
. Para el instante indicado
- Halle la posición del centro de masas (CM) del sistema.
- Calcule la cantidad de movimiento del sistema.
- Halle el momento cinético respecto al origen y respecto al CM.
- Calcule la energía cinética del sistema respecto a un sistema fijo y respecto al CM.
- Halle la aceleración de cada masa y la del CM.
- Halle la derivada respecto al tiempo del momento cinético (calculado respecto al origen).
- Calcule la derivada respecto al tiempo de la energía cinética del sistema (calculada respecto a un sistema fijo).
2 Posición del centro de masas
La posición del centro de masas (CM) es la media ponderada de las tres posiciones
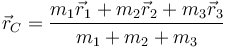
Sustituyendo los diferentes valores
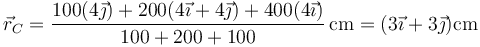
3 Cantidad de movimiento
La cantidad de movimiento de un sistema es la suma de la de cada una de las partículas que lo componen
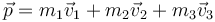
y su valor en este caso es
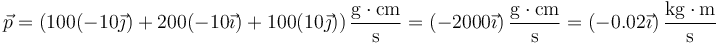
A partir de la cantidad de movimiento podemos hallar la velocidad del CM dividiendo por la masa total
\vec{v}_C = \frac{\vec{p}{M}=\left(\frac{-2000\vec{\imath}}{400}\right)\frac{\mathrm{cm}}{\mathrm{s}}= \left(-5\vec{\imath}\right)\frac{\mathrm{cm}}{\mathrm{s}}
