Propiedades de un sistema de tres partículas
De Laplace
(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Página creada con '==Enunciado== Considere un sistema de tres partículas de masas <math>m_1=100\,\mathrm{g}</math>, <math>m_2=200\,\mathrm{g}</math>, <math>m_3=100\,\mathrm{g}</math> que en un in…')
Edición más nueva →
(Página creada con '==Enunciado== Considere un sistema de tres partículas de masas <math>m_1=100\,\mathrm{g}</math>, <math>m_2=200\,\mathrm{g}</math>, <math>m_3=100\,\mathrm{g}</math> que en un in…')
Edición más nueva →
Revisión de 17:23 24 ene 2013
Contenido |
1 Enunciado
Considere un sistema de tres partículas de masas 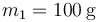 ,
, 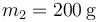 ,
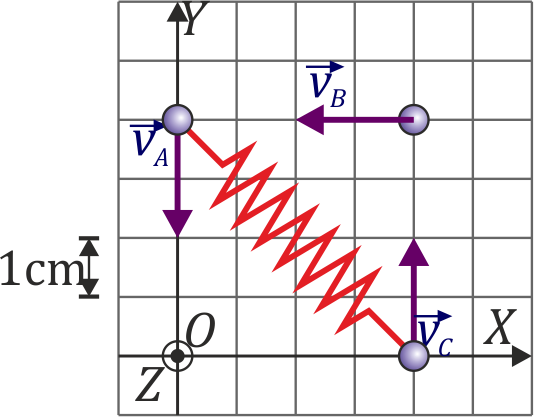
, 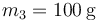 que en un instante dado están situadas en las posiciones de la figura y moviéndose con la velocidad indicada, siendo la rapidez de cada una de ellas
que en un instante dado están situadas en las posiciones de la figura y moviéndose con la velocidad indicada, siendo la rapidez de cada una de ellas  . Suponga
que la masa 1 y la 3 está unidas por un resorte de longitud natural nula y constante
. Suponga
que la masa 1 y la 3 está unidas por un resorte de longitud natural nula y constante 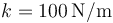 . Para el instante indicado
. Para el instante indicado
- Halle la posición del centro de masas (CM) del sistema.
- Calcule la cantidad de movimiento del sistema.
- Halle el momento cinético respecto al origen y respecto al CM.
- Calcule la energía cinética del sistema respecto a un sistema fijo y respecto al CM.
- Halle la aceleración de cada masa y la del CM.
- Halle la derivada respecto al tiempo del momento cinético (calculado respecto al origen).
- Calcule la derivada respecto al tiempo de la energía cinética del sistema (calculada respecto a un sistema fijo).