Propiedades dinámicas de una esfera en movimiento
De Laplace
(→Momento cinético) |
(→Momento cinético) |
||
| Línea 91: | Línea 91: | ||
<center><math>\vec{L}_O = M(R\vec{k})\times\left(\frac{v_B}{2}\vec{\jmath}\right)+\frac{MRv_B}{5}\left(-\vec{\imath}+\vec{k}\right) = MRv_B\left(-\frac{7}{10}\vec{\imath}+\frac{1}{5}\vec{k}\right)</math></center> | <center><math>\vec{L}_O = M(R\vec{k})\times\left(\frac{v_B}{2}\vec{\jmath}\right)+\frac{MRv_B}{5}\left(-\vec{\imath}+\vec{k}\right) = MRv_B\left(-\frac{7}{10}\vec{\imath}+\frac{1}{5}\vec{k}\right)</math></center> | ||
| + | ;Caso (c): Respecto al CM | ||
| + | <center><math>\vec{L}_C=I\vec{\omega}=\left(\frac{2}{5}MR^2\right)\left(\frac{v_B}{R}\vec{k}\right)=\frac{2MRv_B}{5}\vec{k}</math></center> | ||
| + | |||
| + | :Respecto al punto O tiene este mismo valor por ser nula la velocidad del CM | ||
| + | |||
| + | <center><math>\vec{L}_O=\vec{L}_C=\frac{2MRv_B}{5}\vec{k}</math></center> | ||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
última version al 01:03 18 ene 2013
Contenido |
1 Enunciado
Para las tres casos del problema “Diferentes movimientos de una esfera”
- Calcule la cantidad de movimiento de la esfera.
- Halle la energía cinética de la esfera respecto a su centro y respecto al sistema fijo de ejes.
- Calcule el momento cinético respecto al centro de la esfera y respecto al punto contacto con el suelo.
Dato: Momento de inercia de una esfera de masa M y radio R respecto a un eje que pasa por su centro:

2 Cantidad de movimiento
La cantidad de movimiento de un sólido rígido es igual a la masa del sólido multiplicada por la velocidad del centro de masas

En este caso el centro de masas se halla en el centro de la esfera. La velocidad de este punto se calcula en el problema mencionado. Esto nos da para los tres casos:
- Caso (a)
- La velocidad del centro es la misma que la del punto B y
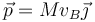
- Caso (b)
- La velocidad de C es la mitad que la de B
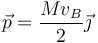
- Caso (c)
- El centro está en el eje de rotación y su velocidad es nula
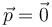
- En el caso del sólido, a diferencia del de una partícula, el que la cantidad de movimiento se anula no implica que el sólido esté en reposo. Solo lo está su centro de masas, pero el sólido puede estar rotando alrededor de éste.
3 Energía cinética
La energía cinética de un sólido se compone de dos partes, una de traslación con el centro de masas y una de rotación alrededor del centro de masas
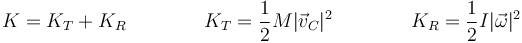
Cuando hablamos de energía cinética respecto al centro de masas nos referimos al segundo término, KR mientras que si hablamos de la energía respecto a un sistema fijo, nos referimos a la suma de los dos términos.
En el caso de una esfera, el momento de inercia respecto a cualquier eje que pase por su centro vale 2MR²/5, por lo que para los tres casos tenemos:
- Caso (a)
- La energía cinética de rotación, que es la que se mide desde el centro de masas es
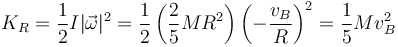
- y la total, que es la que se mide respecto a un sistema fijo
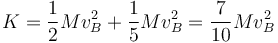
- Caso (b)
- La energía cinética de rotación es ahora
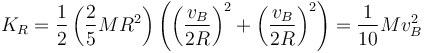
- y la total
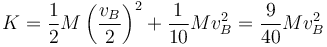
- Caso (c)
- La de rotación es la misma que en el caso (a)

- y la total coincide con esta ya que en este caso el centro de masas está en reposo.
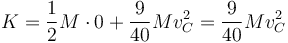
4 Momento cinético
El momento cinético tiene una descomposición similar a la energía cinética

La primera parte se debe al movimiento con el centro de masas y el segundo al movimiento alrededor de él. Este segundo término puede escribirse

Así tenemos, para los tres casos:
- Caso (a)
- Respecto al centro de masas
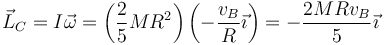
- y respecto al punto de contacto O
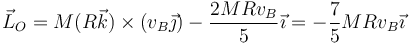
- Caso (b)
- En este caso, el momento cinético respecto al CM
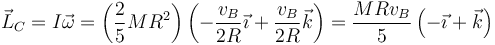
- Respecto al punto O

- Caso (c)
- Respecto al CM
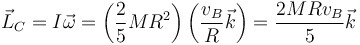
- Respecto al punto O tiene este mismo valor por ser nula la velocidad del CM