Diferentes movimientos de una esfera
De Laplace
(→Tipos de movimiento) |
(→Caso (a)) |
||
| Línea 38: | Línea 38: | ||
==Velocidad angular== | ==Velocidad angular== | ||
===Caso (a)=== | ===Caso (a)=== | ||
| + | En el primer caso, las velocidades de A y B son iguales | ||
| + | |||
| + | <center><math>\vec{v}_A=\vec{v}_B=v_B\vec{\jmath}</math></center> | ||
| + | |||
| + | Esto quiere decir que el eje instantáneo de rotación es paralelo a la recta que pasa por A y B. Dado que | ||
| + | |||
| + | \overrightarrow{AB}=\vec{r}_B-\vec{r}_A = | ||
| + | |||
===Caso (b)=== | ===Caso (b)=== | ||
Revisión de 16:13 17 ene 2013
Contenido |
1 Enunciado
Considérese una esfera de masa M y radio R que se mueve sobre la superficie horizontal z = 0. Consideramos un instante en el que la esfera toca el suelo justo en el origen de coordenadas, O, y tal que en ese momento la velocidad de dicho punto de contacto con el suelo es nula
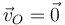
Para este mismo instante la velocidad de los puntos 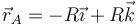 y
y 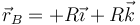 situados en un diámetro horizontal valen respectivamente
situados en un diámetro horizontal valen respectivamente

Para los tres casos siguientes:
- (a) vA = + vB
- (b) vA = 0
- (c) vA = − vB
- Indique justificadamente el tipo de movimiento instantáneo que realiza la esfera (traslación, rotación, helicoidal,…)
- Calcule la velocidad angular del sólido.
- Halle la velocidad angular de pivotamiento y la de rodadura de la esfera.
- Dé la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o de rotación, en su caso).
- Calcule la velocidad lineal del centro C de la esfera y la del punto D situado en el extremo superior de la esfera.
2 Tipos de movimiento
En los tres casos se cumple lo siguiente:
- Hay un punto, el de contacto, que tiene velocidad nula
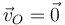
- Existe al menos un punto que tiene una velocidad no nula
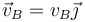
Por tanto, en los tres casos, el movimiento instantáneo es una rotación alrededor de un eje que pasa por O. (no puede ser uno de reposo, pues hay puntos en movimiento, ni una traslación, por ser diferentes las velocidades, ni helicoidal, por haber alguno con velocidad nula).
Lo que cambiará de un caso a otro s la dirección del eje y el valor de la velocidad angular.
3 Velocidad angular
3.1 Caso (a)
En el primer caso, las velocidades de A y B son iguales
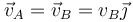
Esto quiere decir que el eje instantáneo de rotación es paralelo a la recta que pasa por A y B. Dado que
\overrightarrow{AB}=\vec{r}_B-\vec{r}_A =





