Diferentes movimientos de una esfera
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Considérese una esfera de masa <math>M</math> y radio <math>R</math> que se mueve sobre la superficie horizontal <math>z=0</math>. Consideramos un instante en el …') |
|||
| Línea 11: | Línea 11: | ||
Para los tres casos siguientes: | Para los tres casos siguientes: | ||
| - | <ol | + | <ol type="a"> |
<li> <math>v_A=+v_B</math></li> | <li> <math>v_A=+v_B</math></li> | ||
<li><math>v_A=0</math></li> | <li><math>v_A=0</math></li> | ||
Revisión de 11:36 17 ene 2013
Contenido |
1 Enunciado
Considérese una esfera de masa M y radio R que se mueve sobre la superficie horizontal z = 0. Consideramos un instante en el que la esfera toca el suelo justo en el origen de coordenadas, O, y tal que en ese momento la velocidad de dicho punto de contacto con el suelo es nula
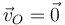
Para este mismo instante la velocidad de los puntos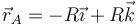 
y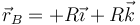 
situados en un diámetro horizontal valen respectivamente
Para los tres casos siguientes:
- vA = + vB
- vA = 0
- vA = − vB<(li>
- Indique justificadamente el tipo de movimiento instantáneo que realiza la esfera (traslación, rotación, helicoidal,…)
- Calcule la velocidad angular del sólido.
- Halle la velocidad angular de pivotamiento y la de rodadura de la esfera.
- Dé la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o de rotación, en su caso).
- Calcule la velocidad lineal del centro C de la esfera y la del punto D situado en el extremo superior de la esfera.
