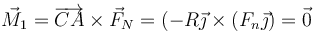Deslizamiento y rodadura de un disco
De Laplace
(→Velocidad del centro de masas) |
|||
| Línea 51: | Línea 51: | ||
Esta aceleración es constante, por lo que su integración nos da una velocidad que disminuye linealmente con el tiempo | Esta aceleración es constante, por lo que su integración nos da una velocidad que disminuye linealmente con el tiempo | ||
| - | <center><math>v_C = v_0-\mu g t</math></center> | + | <center><math>v_C = v_0-\mu g t\,</math></center> |
| + | |||
| + | ===Velocidad angular=== | ||
| + | Para hallar la velocidad angular aplicamos el teorema del momento cinético para el centro de masas | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\vec{L}_C}{\mathrm{d}t}=\vec{M}_C</math></center> | ||
| + | |||
| + | En el caso del movimiento plano de un disco, su momento cinético es proporcional a su velocidad angular, que apunta en la dirección normal al plano | ||
| + | |||
| + | <center><math>\vec{L}_C=I\vec{\omega}=I\omega\vec{k}</math></center> | ||
| + | |||
| + | siendo <math>I</math> el momento de inercia del disco respecto a un eje perpendicular por su centro. | ||
| + | |||
| + | <center><math>I = \frac{1}{2}MR^2</math></center> | ||
| + | |||
| + | Por tanto nos queda, para el primer miembro | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\vec{L}_C}{\mathrm{d}t} = I\alpha\vec{k}</math></center> | ||
| + | |||
| + | siendo <math>\alpha = \dot{\omega}</math> la aceleración angular del disco. | ||
| + | |||
| + | Esta cantidad debe ser igual al momento de las fuerzas que actúan sobre el disco | ||
| + | |||
| + | <center><math>\vec{M}_C = \sum_i \overrightarrow{CP}_i\times\vec{F}_i</math></center> | ||
| + | |||
| + | Debemos hallar el momento de las tres fuerzas y no solo de la de rozamiento, porque aunque la suma del peso y la fuerza normal sea nula, pueden formar un par de fuerzas no nulo. | ||
| + | |||
| + | * El momento del peso es nulo, ya que se aplica en el propio centro de masas | ||
| + | |||
| + | <center><math>\vec{M}_1 = \overrightarrow{CC}\times (M\vec\overrightarrow}) = \vec{0}</math></center> | ||
| + | |||
| + | * El de la fuerza normal también es cero, ya que aunque se aplica en el punto de contacto A, su dirección es la de una recta que pasa por el CM, con lo que el brazo del par es nulo | ||
| + | |||
| + | <center><math>\vec{M}_1 = \overrightarrow{CA}\times \vec{F}_N = (-R\vec{\jmath}\times(F_n\vec{\jmath})=\vec{0}</math></center> | ||
| + | |||
==Velocidad del centro del disco== | ==Velocidad del centro del disco== | ||
==Velocidad del punto superior== | ==Velocidad del punto superior== | ||
Revisión de 21:18 4 ene 2013
Contenido |
1 Enunciado
Por un suelo horizontal se lanza un disco macizo de masa M y radio R. Inicialmente el disco no gira, sino que se desliza con velocidad v0. Si el coeficiente de rozamiento dinámico con el suelo vale μ, ¿cuánto tarda el disco en dejar de deslizar y empezar a rodar sin deslizar? Estudie cómo cambian durante el proceso las siguientes magnitudes:
- Velocidad del centro del disco.
- Velocidad del punto superior del disco.
- Energía cinética de traslación del disco.
- Energía cinética de rotación.
- Energía cinética total.
¿Cómo cambian los resultados si en lugar de un disco macizo tenemos un aro de radio R? ¿Y si tenemos una bola maciza de radio R?
2 Introducción
Para entender la física del problema es preciso entender que en el disco se producen dos efectos opuestos.
Sobre el disco actúan tres fuerzas
- Su peso, en la vertical, perpendicular al plano de contacto.
- La reacción normal del plano
- La fuerza de rozamiento dinámico, proporcional a la fuerza normal.
De estas, puesto que el movimiento del CM es horizontal, el peso y la reacción normal deben compensarse, por lo que la única fuerza relevante es la de rozamiento dinámico.
Esta fuerza de rozamiento es la que tiene un doble efecto:
- Por un lado es una fuerza en el sentido opuesto al movimiento, por lo que debe acelerar al CM del disco hacia atrás
- Por otro, su momento respecto al CM produce un par que hace girar al disco hacia adelante, acelerando al CM hacia adelante.
De la composición de estos dos efectos contrapuestos obtenemos el movimiento del disco. El disco avanza cada vez más lentamente, pero al mismo tiempo gira cada vez más rápido. Llega un momento en que la velocidad del punto de contacto entre el disco y el suelo se anula. En ese momento el disco ya no desliza, solo rueda. A partir de ese instante, ya no hay fuerza de rozamiento dinámíco, sino de rodadura (que es mucho menor) y el movimiento continúa como de solo rodadura. A nosotros nos interesa el proceso hasta ese momento.
3 Tiempo para empezar a rodar
Vamos a calcular la evolución de la velocidad del CM y de la velocidad angular con que gira el disco alrededor de éste. Con estos dos datos, hallamos la velocidad del punto de contacto como función del tiempo. El tiempo hasta que empiece a rodar nos lo da el que esta velocidad se anule.
3.1 Velocidad del centro de masas
La aceleración del centro de masas nos la da el teorema de la cantidad de movimiento
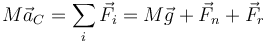
Descomponiendo en las componentes X e Y queda
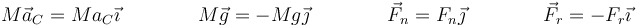
Igualando componente a componente nos quedan las dos ecuaciones escalares

Por tratarse de una situación de rozamiento dinámico

Esta aceleración es constante, por lo que su integración nos da una velocidad que disminuye linealmente con el tiempo
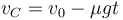
3.2 Velocidad angular
Para hallar la velocidad angular aplicamos el teorema del momento cinético para el centro de masas

En el caso del movimiento plano de un disco, su momento cinético es proporcional a su velocidad angular, que apunta en la dirección normal al plano

siendo I el momento de inercia del disco respecto a un eje perpendicular por su centro.
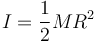
Por tanto nos queda, para el primer miembro

siendo 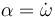 la aceleración angular del disco.
la aceleración angular del disco.
Esta cantidad debe ser igual al momento de las fuerzas que actúan sobre el disco
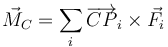
Debemos hallar el momento de las tres fuerzas y no solo de la de rozamiento, porque aunque la suma del peso y la fuerza normal sea nula, pueden formar un par de fuerzas no nulo.
- El momento del peso es nulo, ya que se aplica en el propio centro de masas
- El de la fuerza normal también es cero, ya que aunque se aplica en el punto de contacto A, su dirección es la de una recta que pasa por el CM, con lo que el brazo del par es nulo