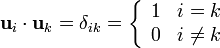Base ortonormal dextrógira
De Laplace
(Diferencias entre revisiones)
(→...ortogonales,...) |
(→...ortogonales,...) |
||
| Línea 16: | Línea 16: | ||
La condición de ortonormalidad (carácter unitario más ortogonalidad) se puede expresar de forma compacta con ayuda de la Delta de Kronecker | La condición de ortonormalidad (carácter unitario más ortogonalidad) se puede expresar de forma compacta con ayuda de la Delta de Kronecker | ||
| - | <center><math>\mathbf{u}_i\cdot\mathbf{u}_k = \delta_{ik} | + | <center><math>\mathbf{u}_i\cdot\mathbf{u}_k = \delta_{ik} = \left\{\begin{array}{ll}1 & i=k \\ 0 & i\neq k\end{array}\right.</math></center> |
| - | + | ||
| - | + | ||
Revisión de 17:40 21 nov 2007
1 Definición
Una base vectorial se dice que es ortonormal dextrógira, si sus vectores son unitarios, ortogonales, y verifican la regla de la mano derecha.
2 Vectores unitarios,...
Un vector es unitario cuando su módulo es la unidad. Matemáticamente, esto quiere decir que si la base vectorial es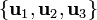 
se cumple
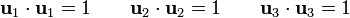
3 ...ortogonales,...
Una base es ortonormal cuando además de ser unitaria, sus vectores son ortogonales entre sí. Esto se expresa como
La condición de ortonormalidad (carácter unitario más ortogonalidad) se puede expresar de forma compacta con ayuda de la Delta de Kronecker
