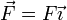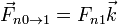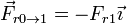Dos bloques apilados

De Laplace

(Diferencias entre revisiones)

Revisión de 14:48 21 nov 2012

Contenido

1 Enunciado
2 Introducción
3 Diagramas de cuerpo libre
4 Componentes verticales
5 Caso sin rozamiento con la mesa
- 5.1 Bloques solidarios
- 5.2 Bloques separados
6 Caso general
7 Casos prácticos

1 Enunciado

Sobre una mesa horizontal se encuentran apilados dos bloques, siendo el inferior de masa $m 1$ y el superior de masa $m 2$ . El coeficiente de rozamiento estático del bloque inferior con la mesa vale $μ 1$ y el del segundo bloque con el primero $μ 2$ . Los coeficientes de rozamiento dinámico valen lo mismo que los estáticos.

Para el estado de reposo y sin fuerzas laterales aplicadas, indique la fuerza que la mesa ejerce sobre el bloque inferior y el que éste ejerce sobre el superior.
Suponiendo $μ 1 = 0$ , se tira del bloque inferior con una fuerza horizontal $F$ . ¿Qué fuerzas actúan sobre cada bloque? ¿Cuánto debe valer como mínimo esta fuerza si se quiere que el bloque superior se quede atrás? ¿Cuánto vale la aceleración de cada bloque para valores de la fuerza inferiores o superiores a este valor crítico?
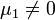Resuelva las mismas cuestiones que en el apartado anterior, suponiendo ahora $\mu_1\neq 0$ .
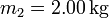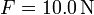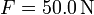
Calcule los valores de las diferentes fuerzas y las aceleraciones si $m_1 = 3.00\,\mathrm{kg}$ , $m_2 = 2.00\,\mathrm{kg}$ , $μ 1 = 0.30$ , $μ 2 = 0.50$ para (a) $F=10.0\,\mathrm{N}$ (b) $F=20.0\,\mathrm{N}$ (c) $F=50.0\,\mathrm{N}$

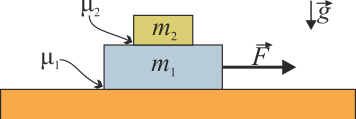
2 Introducción

Este problema es una versión simplificada del conocido problema de con qué fuerza debe tirarse de un mantel si se desea que los platos y vasos queden por detrás. En un problema realista, las copas y vasos deben considerarse como sólidos, no partículas, ya que lo más probable es que vuelquen. En primera aproximación, no obstante, podemos considerar solo el efecto del deslizamiento relativo.

Es conocido que si se tira del bloque inferior con una fuerza pequeña, pero suficiente para vencer el rozamiento con la mesa, el bloque superior se moverá solidariamente con el inferior. La pregunta que nos podemos hacer es ¿qué fuerza mueve al bloque superior? La respuesta es que la única que actúa sobre ella en la dirección horizontal es el rozamiento con el bloque inferior. Por tanto, aquí tenemos un ejemplo sencillo en el que el rozamiento no se opone al movimiento sino que por el contrario es su causa. A los que se opone el movimiento relativo, esto es, a que el bloque 2 se mueva respecto al 1 (y viceversa)

3 Diagramas de cuerpo libre

Cuando tenemos un sistema formado por varias partes, la técnica de solución pasa por dibujar los diagramas de cuerpo libre, en los que cada elemento se representa por separado, indicando todas las fuerzas a que está sometido. Entre las fuerzas aplicadas se incluyen las de reacción vincular, debidas a contactos y ligaduras.

En este caso tenemos los dos bloque s que denominaremos “1” y “2”, respectivamente. A la mesa, en el que está apoyado el bloque 1, lo etiquetaremos como “0”.

Así tenemos, para el bloque 1, las siguientes fuerzas:

Su peso, 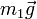$m_1\vec{g}$ causado por la atracción terrestre.
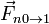La fuerza de reacción normal ejercida por el plano, $\vec{F}_{n0\to 1}$ .
La fuerza de reacción normal debida al bloque superior, 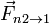$\vec{F}_{n2\to 1}$ . Nótese que esta fuerza no es “el peso del bloque 2” (ya que el peso de 2 es una fuerza ejercida por la tierra sobre el bloque 2. La fuerza normal de que hablamos es la fuerza elástica debida al contacto entre los dos bloques. Otra cosa es que su valor sea igual a peso de ese bloque.
la fuerza aplicada $\vec{F}$
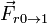La fuerza de rozamiento debida a la mesa, $\vec{F}_{r0\to 1}$ .
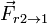La fuerza de rozamiento debida al bloque 2, $\vec{F}_{r2\to 1}$ .

De estas seis fuerzas, las tres primeras son verticales y las tres últimas horizontales.

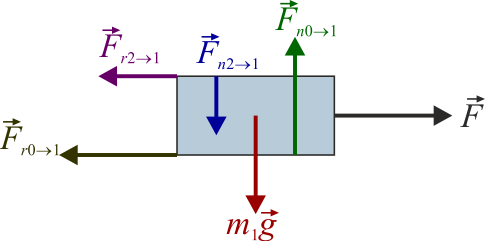
Nótese que, puesto que estamos tratando el bloque como una partícula, no importa el punto de aplicación de cada una. Es equivalente a que todas se apliquen en el centro de masas del bloque.

La suma de todas ellas nos da la aceleración de la masa 1

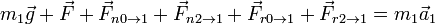
$m_1\vec{g}+\vec{F}+\vec{F}_{n0\to 1}+\vec{F}_{n2\to 1}+\vec{F}_{r0\to 1} + \vec{F}_{r2\to 1} = m_1\vec{a}_1$

Sobre el bloque 2 actúan menos fuerzas:

Su peso, 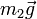$m_2\vec{g}$ causado por la atracción terrestre.
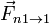La fuerza de reacción normal debida al bloque inferior, $\vec{F}_{n1\to 1}$ .
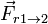La fuerza de rozamiento debida al bloque 1, $\vec{F}_{r1\to 2}$ .

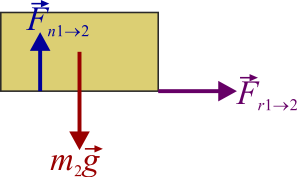
Por aplicación de la segunda ley de Newton nos da

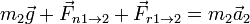
$m_2\vec{g}+\vec{F}_{n1\to 2}+ \vec{F}_{r1\to 2} = m_2\vec{a}_2$

Por la tercera ley de Newton se cumple

$\vec{F}_{n1\to 2} = -\vec{F}_{n2\to 1}\qquad\qquad \vec{F}_{n1\to 2} = -\vec{F}_{n2\to 1}$

Empleando componentes según un sistema de ejes con el OX paralelo a la mesa y OZ perpendicular a ella nos quedan las descomposiciones

$\vec{F}=F\vec{\imath}$

$m_1\vec{g}=-m_1g\vec{k}\qquad m_2\vec{g}=-m_2g\vec{k}$

$\vec{F}_{n0\to 1} = F_{n1}\vec{k}$

$\vec{F}_{n2\to 1}=-F_{n2}\vec{k}\qquad \vec{F}_{n1\to 2}=+F_{n2}\vec{k}$

$\vec{F}_{r0\to 1} = -F_{r1}\vec{\imath}$

$\vec{F}_{r2\to 1}=-F_{r2}\vec{\imath}\qquad \vec{F}_{n1\to 2}=+F_{r2}\vec{\imath}$

$m_1\vec{a}_1=m_1a_1\vec{\imath}\qquad m_2\vec{a}_2=m_2a_2\vec{\imath}$

Hay que destacar que, en las expresiones anteriores no se presupone que las diferentes cantidades $F n 1$ , $F r 1$ sean todas positivas. Simplemente se les ha asignado una dirección, pero su sentido podría ser el supuesto o el opuesto, si resulta una cantidad negativa. Por supuesto, ayuda el que desde el principio se suponga el sentido adecuado y resulten cantidades exclusivamente positivas.

Llevando esto a las ecuaciones de movimiento e igualando componente a componente queda, para el bloque 1

$-m_1g+F_{n1}-F_{n2}=0\qquad\qquad F-F_{r1}-F_{r2} = m_1a_1$

y para el bloque 2

$-m_2g + F_{n2} = 0 \qquad\qquad F_{r2}=m_2a_2$

4 Componentes verticales

Puesto que no hay movimiento en la dirección vertical, las componentes de las fuerzas en esta dirección se equilibran unas a otras. Nos queda

$-m_1g+F_{n1}-F_{n2}=0\qquad\qquad -m_2g + F_{n2} = 0$

de donde hallamos los valores de las fuerzas normales

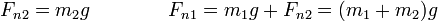
$F_{n2} = m_2g\qquad\qquad F_{n1}= m_1g+F_{n2}= (m_1+m_2)g$

El resultado es el que cabe esperar. La reacción normal del bloque inferior iguala al peso que soporta, debido al bloque superior, mientras que la rección de la mesa iguala al peso de los dos bloques juntos.

5 Caso sin rozamiento con la mesa

Para las fuerzas horizontales ya puede haber movimiento, por lo que las ecuaciones no son de equilibrio, sino que nos permiten hallar las aceleraciones con que se mueven lo bloques.

Suponemos en primer lugar, para hacer el problema más simple, que no hay rozamiento con la mesa. En este caso

$F_{r1}=0\,$

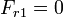
lo que nos deja con las ecuaciones para la componente horizontal

$F-F_{r2} = m_1a_1\qquad\qquad F_{r2}=m_2a_2\qquad \qquad$

Esto es un sistema de dos ecuaciones con tres incógnitas ( $F r 2$ , $a 1$ y $a 2$ ), por lo que no nos basta para resolver el problema.

Tenemos dos posibilidades, dependiendo de la magnitud de la fuerza aplicada: que los bloques se muevan al unísono o separadamente.

5.1 Bloques solidarios

Cuando la fuerza es pequeña, los dos bloques se mueven conjuntamente. En este caso

$a_1 = a_2\,$

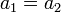
lo que ya permite resolver el sistema. Sumando las dos ecuaciones

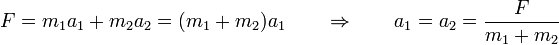
$F = m_1a_1 + m_2 a_2 = (m_1+m_2)a_1 \qquad\Rightarrow\qquad a_1 = a_2 = \frac{F}{m_1+m_2}$

Puesto que los dos bloques se mueven como uno solo, la aceleración que adquieren es igual a la fuerza aplicada dividida por la masa total.

La fuerza de rozamiento la hallamos de cualquiera de las dos ecuaciones

$F_{r2}=m_2a_2 = \frac{m_2}{m_1+m_2}F$

Esta fuerza de rozamiento aumenta a medida que lo hace la fuerza aplicada. Ahora bien, de acuerdo con las leyes del rozamiento seco, este crecimiento no puede ser ilimitado, ya que debe cumplirse que

$|\vec{F}_{r2}| \leq \mu_2 |\vec{F}_{n2}| =\mu m_2 g$

Esta condición nos da el valor de la máxima fuerza que arrastra a los dos bloques a la vez

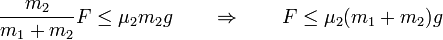
$\frac{m_2}{m_1+m_2}F \leq \mu_2 m_2 g \qquad \Rightarrow \qquad F\leq \mu_2(m_1+m_2)g$

5.2 Bloques separados

Una vez que se supera el valor crítico

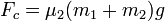
$F_c = \mu_2(m_1+m_2)g\,$

ya los dos bloques adquieren aceleraciones diferentes, ya que el superior no es capaz de seguir al inferior.

En este caso, el rozamiento entre los dos bloques no es estático sino dinámico, ya que existe movimiento relativo. En este caso la fuerza de rozamiento es prácticamente constante y proporcional a la fuerza normal

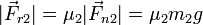
$|\vec{F}_{r2}| = \mu_2 |\vec{F}_{n2}| = \mu_2m_2g$

(suponemos que el coeficiente de rozamiento dinámico es igual al estático. Esta ecuación nos permite determinar las dos aceleraciones, ya que

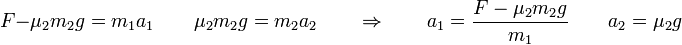
$F-\mu_2m_2g = m_1 a_1\qquad \mu_2m_2g = m_2a_2\qquad\Rightarrow\qquad a_1 = \frac{F-\mu_2m_2g}{m_1}\qquad a_2 = \mu_2 g$

Podemos comprobar que las dos aceleraciones se igualan cuando la fuerza iguala a su valor crítico

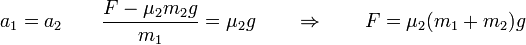
$a_1 = a_2 \qquad \frac{F-\mu_2m_2g}{m_1}=\mu_2 g\qquad\Rightarrow\qquad F = \mu_2(m_1+m_2)g$

6 Caso general

Supongamos ahora que también hay rozamiento entre el bloque y la mesa. En este caso, las ecuaciones de movimiento horizontales se convierten en:

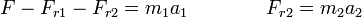
$F-F_{r1}-F_{r2} = m_1a_1\qquad\qquad F_{r2}=m_2a_2\qquad \qquad$

Pero a la vista de este sistema, vemos que es exactamente el mismo que el de la sección anterior si definimos una fuerza efectiva

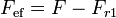
$F_\mathrm{ef} = F-F_{r1}\,$

esto es que lo que cuenta no es el valor de la fuerza aplicada sino en cuánto supera a la fuerza de rozamiento.

Tenemos entonces los tres casos siguientes.

6.1 Reposo

Cuando la fuerza aplicada es muy pequeña, no es capaz de superar al rozamiento estático, que la iguala, y los bloques permanecen en reposo. Esto ocurre cuando

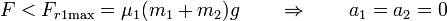
$F < F_{r1\mathrm{max}} = \mu_1 (m_1+m_2)g\qquad\Rightarrow\qquad a_1 = a_2 = 0$

6.2 Movimiento solidario

Cuando la fuerza sobrepasa este umbral ya se produce movimiento de los bloques. El rozamiento entre el bloque 1 y la mesa es dinámico y prácticamente independiente de la velocidad, lo que nos da la fuerza efectiva

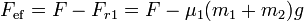
$F_\mathrm{ef}=F-F_{r1}=F-\mu_1(m_1+m_2)g\,$

y las aceleraciones

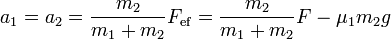
$a_1=a_2 = \frac{m_2}{m_1+m_2}F_\mathrm{ef} = \frac{m_2}{m_1+m_2}F-\mu_1 m_2g$

6.3 Movimiento separado

El movimiento solidario se rompe cuando la fuerza efectiva supera su valor crítico

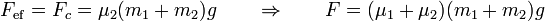
$F_\mathrm{ef} = F_c = \mu_2(m_1+m_2)g \qquad\Rightarrow\qquad F = (\mu_1+\mu_2)(m_1+m_2)g$

a partir de ese momento cada uno de los bloques tiene su propia aceleración

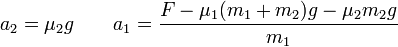
$a_2 = \mu_2 g\qquad a_1 = \frac{F-\mu_1(m_1+m_2)g-\mu_2m_2g}{m_1}$

7 Casos prácticos

Para los datos del enunciado tenemos que los pesos de las dos masas valen

$m_1 g = 29.4\,\mathrm{N}\qquad m_2g = 19.6\,\mathrm{N}$

y por tanto las dos fuerzas normales son iguales a

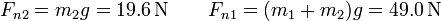
$F_{n2}=m_2g = 19.6\,\mathrm{N}\qquad F_{n1}=(m_1+m_2)g=49.0\,\mathrm{N}$

Esto nos da los dos valores máximos para las fuerzas de rozamiento

$F_{r1\mathrm{max}}=\mu_1F_{n1} = 14.7\,\mathrm{N}\qquad\qquad F_{r2\mathrm{max}}=\mu_2F_{n2}= 9.80\,\mathrm{N}$

Tenemos entonces las tres situaciones:

Reposo: Si la fuerza aplicada es menor de 14.7 N el estado es de reposo. Este es el caso para una fuerza aplicada de 10 N (caso a)

Movimiento solidario: Para

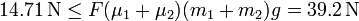
$14.71\,\mathrm{N}\leq F (\mu_1+\mu_2)(m_1+m_2)g = 39.2\,\mathrm{N}$

los dos bloques se mueven conjuntamente. Este es el caso (B), en el que la fuerza aplicada vale 20 N. Para esta fuerza aplicada, la fuerza efectiva vale

$F_\mathrm{ef}=(20.0-14.7)\,\mathrm{N}=5.29\,\mathrm{N}$

lo que nos da las aceleraciones

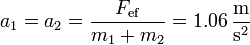
$a_1 = a_2 = \frac{F_\mathrm{ef}}{m_1+m_2} = 1.06\,\frac{\mathrm{m}}{\mathrm{s}^2}$

y las fuerzas de rozamiento

$F_{r1} = \mu_1(m_1+m_2)g = 14.7\,\mathrm{N}\qquad F_{r2}=m_2 a_2 = 2.12\,\mathrm{N}$

Movimiento separado: Si

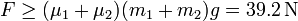
$F\geq (\mu_1+\mu_2)(m_1+m_2)g = 39.2\,\mathrm{N}$

los bloques se separan. Este es el caso (c), correspondiente a una fuerza de 50 N. Las aceleraciones resultantes valen

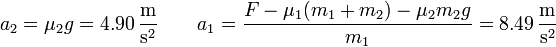
$a_2 = \mu_2g = 4.90\,\frac{\mathrm{m}}{\mathrm{s}^2}\qquad a_1 = \frac{F-\mu_1(m_1+m_2)-\mu_2m_2g}{m_1}=8.49\,\frac{\mathrm{m}}{\mathrm{s}^2}$

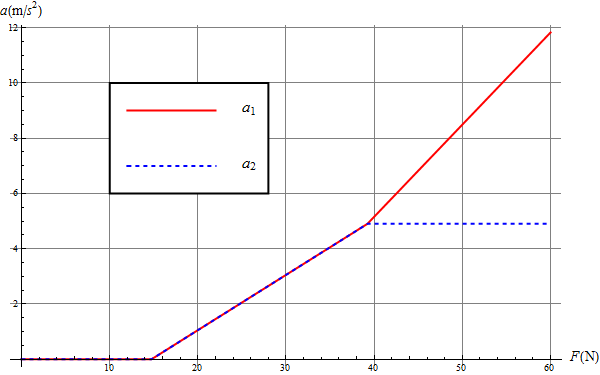
Gráficamente tenemos un comportamiento como el de la figura.

Dos bloques apilados

De Laplace

Revisión de 14:48 21 nov 2012

Contenido

1 Enunciado

2 Introducción

3 Diagramas de cuerpo libre

4 Componentes verticales

5 Caso sin rozamiento con la mesa

5.1 Bloques solidarios

5.2 Bloques separados

6 Caso general

6.1 Reposo

6.2 Movimiento solidario

6.3 Movimiento separado

7 Casos prácticos

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

@@ Línea 12: / Línea 12: @@
 Este problema es una versión simplificada del conocido problema de con qué fuerza debe tirarse de un mantel si se desea que los platos y vasos queden por detrás. En un problema realista, las copas y vasos deben considerarse como sólidos, no partículas, ya que lo más probable es que vuelquen. En primera aproximación, no obstante, podemos considerar solo el efecto del deslizamiento relativo.
-Es conocido que si se tira del bloque inferior con una fuerza pequeña, pero suficiente para vencer el rozamiento con la mesa, el bloque superior se moverá solidariamente con el inferior. La pregunta que nos podemos hacer es ¿qué fuerza mueve al bloque superior? La respuesta es que la única que actúa sobre ella en la dirección horizontal es el rozamiento con el bloque inferior. Por tanto, aquí tenemos un ejemplo sencillo en el que el rozamiento no se opone al movimiento sino que por el contrario es su causa. A los que se opone el movimiento relativo, esto es ,a que el bloque 2 se mueva respecto al 1 (y viceversa)
+Es conocido que si se tira del bloque inferior con una fuerza pequeña, pero suficiente para vencer el rozamiento con la mesa, el bloque superior se moverá solidariamente con el inferior. La pregunta que nos podemos hacer es ¿qué fuerza mueve al bloque superior? La respuesta es que la única que actúa sobre ella en la dirección horizontal es el rozamiento con el bloque inferior. Por tanto, aquí tenemos un ejemplo sencillo en el que el rozamiento no se opone al movimiento sino que por el contrario es su causa. A los que se opone el movimiento relativo, esto es, a que el bloque 2 se mueva respecto al 1 (y viceversa)
 ==Diagramas de cuerpo libre==
 Cuando tenemos un sistema formado por varias partes, la técnica de solución pasa por dibujar los diagramas de cuerpo libre, en los que cada elemento se representa por separado, indicando todas las fuerzas a que está sometido. Entre las fuerzas aplicadas se incluyen las de reacción vincular, debidas a contactos y ligaduras.