Rectas de mejor ajuste en Excel
De Laplace
(→Ordenada en el origen, a) |
(→Coeficiente de correlación, r) |
||
| Línea 140: | Línea 140: | ||
<center>[[Archivo:ejemplo-recta-correlacion.png]]</center> | <center>[[Archivo:ejemplo-recta-correlacion.png]]</center> | ||
| - | El resultado en este caso es 0. | + | El resultado en este caso es 0.9998626. Aplicando la regla del redondeo particular para el coeficiente de correlación escribimos |
<center><math>r = 0.9998\,</math></center> | <center><math>r = 0.9998\,</math></center> | ||
Revisión de 11:00 18 nov 2012
Contenido |
1 Introducción
En la mayoría de las prácticas de laboratorio se requiere el trazado de una o varias “rectas de mejor ajuste” o “rectas de mínimos cuadrados” (en nuestro contexto, ambos términos son sinónimos). En este artículo se trata de explicar de forma lo más clara posible qué son, como se calculan y sobre todo, cómo se representan gráficamente de forma correcta. Aparte de las fórmulas, explicaremos el procedimiento particularizado en el programa Excel.
2 Qué es una recta de mejor ajuste
Muchas leyes físicas obedecen un comportamiento lineal, que quiere decir que una variable depende de otra como una función de primer grado. Así, por ejemplo, la ley de Hooke nos relaciona la fuerza aplicada a un muelle con la elongación de éste respecto a la posición de equilibrio)
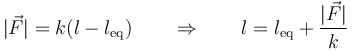
Si esta fuerza la aplicamos colgando sucesivas masas, obtenemos la relación teórica entre longitud del muelle y masa colgada
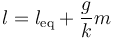
que es un caso particular de relación lineal
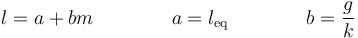
donde a es la llamada ordenada en el origen y b es la pendiente.
Idealmente, si representamos la longitud del resorte frente a la masa obtendremos una recta cuya pendiente es b y que corta el eje de ordenadas a una altura a.
Esta es una ley teórica, que se apoya en evidencias experimentales. Esto quiere decir que si, para un muelle dado, medimos la elongación para distintas masas concretas, deberíamos obtener una serie de puntos alineados. A partir de la recta que pasa por estos puntos podemos determinar la constante k del muelle o su longitud de equilibrio, por ejemplo.
Cuando se tienen dos puntos experimentales, existe solo una recta que pasa por ellos, por lo que con solo dos puntos seríamos capaces de hallar a y b.
Sin embargo, solo dos medidas puede ser demasiado poco. Si han salido mal, por la razón que sea, lo que se deduzca de ellas estará igualmente mal. Por ello, es preferible hacer más medidas, cuantas más mejor. De esta forma, los posibles errores se reducen, ya que si en algunos hemos medido de más, en otros se medirá de menos, y el efecto de una mala medida se amortigua.
El problema es que cuando se tienen más de dos puntos experimentales, ya no habrá una recta que pase por todos ellos, ya que nunca van a estar perfectamente alineados.
Lo que se hace en ese caso es buscar la “recta de mejor ajuste”, que es aquella que probablemente no pase por ninguno de los puntos experimentales, pero es la que, en promedio, pasa más cerca de todos ellos. Una vez calculada la ecuación de esta recta, podemos emplear sus coeficientes para determinar las magnitudes del problema.
3 Por qué se llama “de mínimos cuadrados”
En el contexto de las prácticas de Física usamos indistintamente los términos de “recta de mejor ajuste” y “recta de mínimos cuadrados”, aunque siendo precisos, el segundo término corresponde al método concreto que se emplea para hallar la recta de mejor ajuste (existiendo más de un método).
El principio del método es el siguiente: puesto que no podemos conseguir una recta que pase por todos los puntos experimentales, buscamos una que sea la que pase más cerca de todos ellos.
Supongamos que tenemos un conjunto de datos experimentales 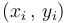 y suponemos una recta, cuya pendiente y ordenada en el origen son aun desconocidas
y suponemos una recta, cuya pendiente y ordenada en el origen son aun desconocidas
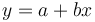
Para un valor xi la diferencia entre lo que predice la recta y lo que se ha medido es el llamado residuo

Un residuo puede ser positivo o negativo. Por ello, si queremos minimizar los residuos, consideramos la suma de sus cuadrados (que son siempre positivos)
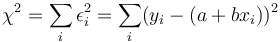
El método de los mínimos cuadrados consiste entonces en hallar los valores de a y b que hacen mínima esta suma de cuadrados. De ahí el nombre del método. El resultado de esta minimización produce los resultados que se ven en las secciones siguientes.
A este método también se lo denomina "regresión lineal" (“linear regression” en inglés), razón por la que en las calculadoras se lo suele identificar como modo LR.
4 Antes de calcular: representando los puntos
4.1 Medidas experimentales
Supongamos que tenemos un resorte del cual vamos suspendiendo diferentes pesos y medimos, para cada pesa, la longitud total del muelle, empleando una regla graduada en milímetros. Obtenemos, tras una serie de medidas, la siguiente tabla:
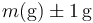
| 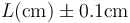
|
|---|---|
| 50 | 15.6 |
| 100 | 15.7 |
| 200 | 15.9 |
| 500 | 16.5 |
| 1000 | 17.4 |
| 2000 | 19.4 |
De una tabla como esta hay que resaltar que en la cabecera hay que indicar las unidades y el error; se entiende que lo que se ponga en la cabecera se aplica a todas las celdas de la columna. Solo si las unidades o errores fueran diferentes para cada dato habría que indicarlo en cada celda
4.2 Implementación en Excel
Para hacer nuestro análisis, abrimos un fichero nuevo de Excel, en el cual introducimos los valores. Por corrección (aunque no hace falta para los cálculos; evita confusiones) añadimos una cabecera con las magnitudes y unidades.
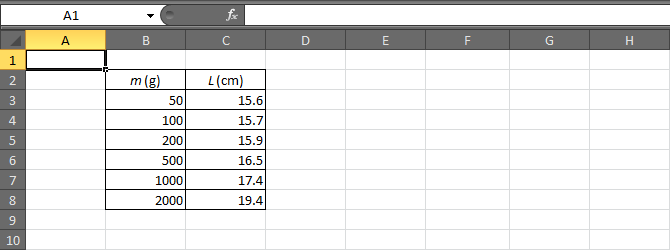
En este ejemplo, los datos de las "x" estarán en las celdas B3 a B8 y los de las "y" de la C3 a la C8. Evidentemente, en cada caso concreto la ubicación de estas celdas cambiará.
4.3 Haciendo una gráfica de los datos
Antes de hacer ningún cálculo, conviene hacer una gráfica de los datos, que refinaremos más tarde. El objeto de esta gráfica es comprobar si los puntos están más o menos alineados o si hay que descartar alguno que se salga de la tendencia.
Para ello, seleccionamos (con el ratón o los cursores) las celdas que contienen los datos y aplicamos la operación de “Insertar” y luego elegimos un gráfico del tipo "Dispersión" (o "XY"), que contiene los puntos experimentales.
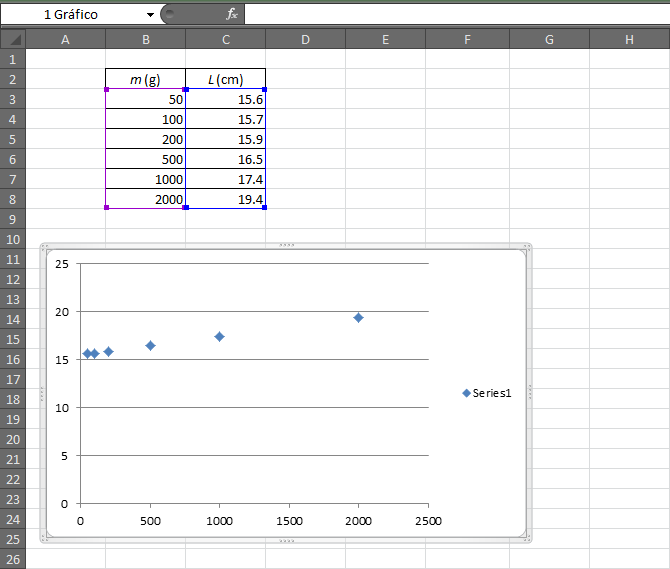
En este ejemplo, los límites de los ejes por defecto que aplica el programa no son los apropiados para ver con claridad si los datos están alineados. Esta es una lección permanente: hacer una gráfica no consiste en aceptar de forma acrítica los resultados de la aplicación. Consiste en ir fijando los parámetros adecuadamente hasta que salga la gráfica deseada.
En nuestro caso, pinchamos con el botón de la derecha del ratón en uno de los números del eje de ordenadas. Esto hace aparecer la opción "Dar formato al eje...". Dentro de esta, podemos seleccionar los límites de los ejes. Puesto que nuestros datos valen como mínimo 15.6 y como máximo 19.4 tomamos como mínimo un valor fijo de 15 y como máximo uno fijo de 20. De esta forma se ve mucho más claro.
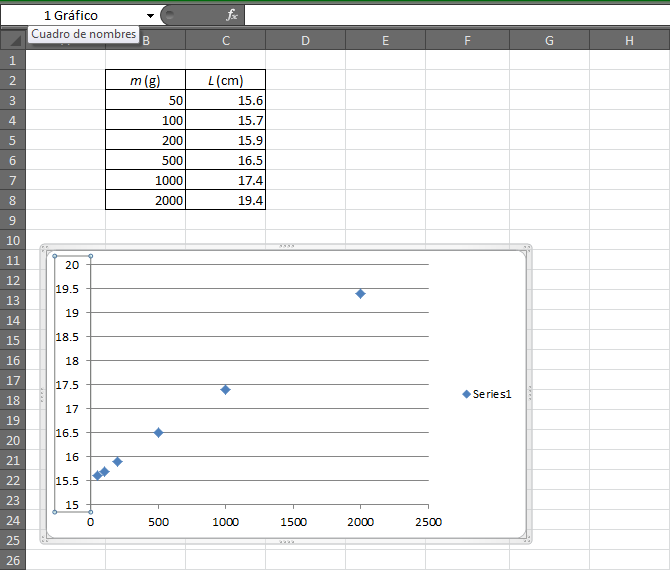
El resultado es que, efectivamente, parece que están alineados, y no hay ningún dato extraño, por lo que podemos continuar con los cálculos.
5 Cómo se calcula
5.1 Pendiente, b
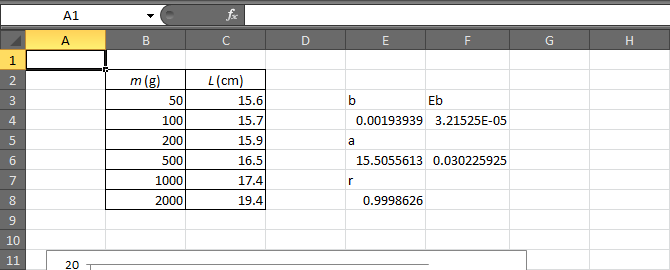
Supongamos que tenemos una lista de datos en dos columnas de una hoja de Excel, que como en la figura, se encuentran en las celdas B3 a B8 (los valores de xi) y de C3 a C8 los de yi. En ese caso la pendiente de la recta de mejor ajuste se calcula con la función PENDIENTE. Escribimos en la celda correspondiente
=PENDIENTE(C3:C8;B3:B8)
donde los argumentos de la función son en primer lugar los datos de las yi y luego los de las xi. Los argumentos se separan por un punto y coma; los extremos de cada columna por dos puntos.
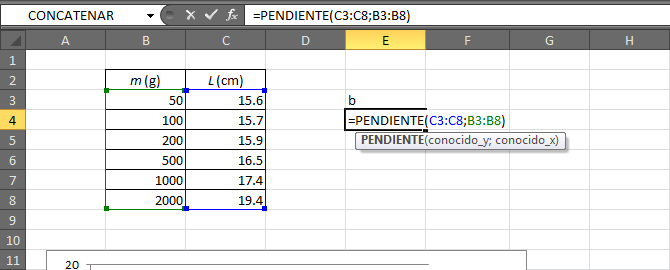
En este caso la operación produce un resultado 0.00193939 (al cual luego le tendremos que hallar el error).
La pendiente es una magnitud con unidades, siendo sus dimensiones las de "y" divididas por las de "x". En este caso sería
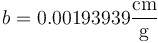
5.2 Ordenada en el origen, a
La ordenada en el origen, a, se halla de manera análoga empleando en este caso la función INTERSECCION.EJE
=INTERSECCION.EJE(C3:C8;B3:B8)
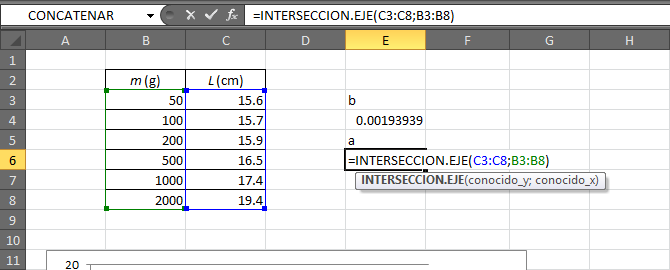
El resultado en este caso es 15.5055613 (que luego redondearemos teniendo en cuenta el error). La ordenada en el origen tiene las mismas dimensiones que “y”, que en este ejemplo es una longitud medida en centímetros, por lo que

5.3 Coeficiente de correlación, r
El tercer parámetro que caracteriza a una recta de mejor ajuste es el coeficiente de correlación. Este mide la “bondad” de la recta. Es un número adimensional comprendido entre -1 y +1. Cuanto más se acerque en valor absoluto a la unidad, mayor es el grado de alineado de los puntos (siendo |r| = 1 una recta perfecta).
En las prácticas de laboratorio de física, los comportamientos lineales son muy precisos por lo que el coeficiente de correlación está muy cerca de 1 casi siempre. En este caso, la verdadera información la obtenemos de cuánto se acerca a la unidad. Para ello, en lugar de redondearlo a partir de un cálculo de errores, lo que hacemos es conservar tantos nueves como contenga tras el punto decimal y la primera cifra que no sea un 9. Así una r = 0.992 sería una recta menos alineada que r = 0.99997, ya que la primera es de solo "dos nueves" y la segunda de "cuatro nueves".
El coeficiente de correlación se calcula de forma similar a la pendiente b y a la ordenada en el origen, a. En este caso se emplea la función COEF.DE.CORREL
=COEF.DE.CORREL(C3:C8;B3:B8)
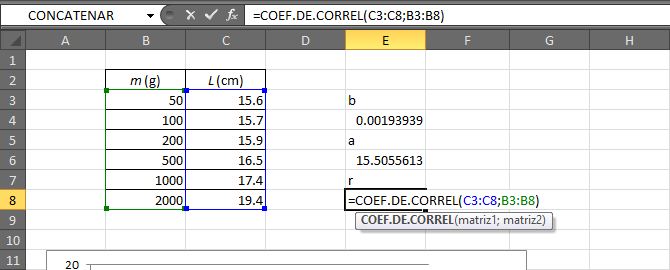
El resultado en este caso es 0.9998626. Aplicando la regla del redondeo particular para el coeficiente de correlación escribimos
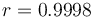
5.4 Incertidumbre de la pendiente, Eb
El cálculo anterior de la pendiente hay que refinarlo calculando la incertidumbre de ésta. Esta incertidumbre se debe tanto al hecho de que cada dato es incierto (por las limitaciones propias del proceso de medida) como al hecho de que se trata de una estimación estadística. Para que fuera exacta deberíamos reunir infinitos datos.
La mejor estimación de la incertidumbre de la pendiente puede hallarse recurriendo de nuevo a un cálculo del mínimo de una función y el resultado es
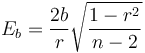
siendo b la propia pendiente, r el coeficiente de correlación y n el número de datos. vemos que cuando n tiende a infinito el error de la pendiente se anula.
Para calcular este error con Excel debemos recurrir a las funciones RAIZ(), que halla la raíz cuadrada y CONTAR(), que nos da el número de datos de la columna (sin incluir las celdas vacías).
En nuestro ejemplo, con los valores en las celdas que hemos empleado, queda
=2*E4/E8*RAIZ((1-E8^2)/(CONTAR(B3:B8)-2))
siendo E4 la casilla donde está almacenada b, y E8 donde está r. Obviamente, en otro ejemplo habrá que cambiar estas referencias por las que correspondan.
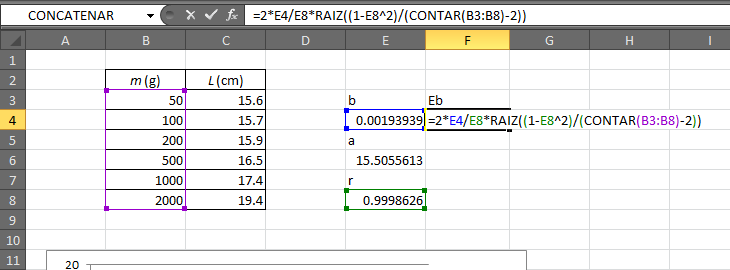
El resultado del cálculo en este caso nos da 2.99083E-05, esto es, 2.99083×10-05. La incertidumbre de b tiene las mismas unidades que b, es decir
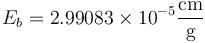
5.5 Expresión de la pendiente con su incertidumbre
Si expresamos b con su incertidumbre nos queda
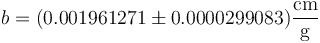
Aplicamos ahora las técnicas del redondeo: colocamos el error bajo la maginitud
0.001961271 0.0000299083
Consideramos las dos primeras cifras significativas del error (29), puesto que son mayores de 25 redondeamos a una cifra
0.001961271 0.00003
Redondeamos ahora la pendiente hasta la cifra en que hemos cortado el error
0.00196 0.00003
Volvemos a escribir la pendiente con su error, ya redondeados:
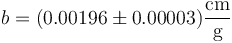
o, en forma compacta
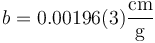
o, en notación científica
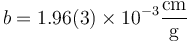
Si ahora pasamos a las magnitudes fundamentales del sistema internacional
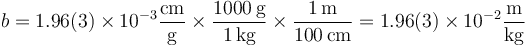
Por tanto, escribiremos en la celda correspondiente del formulario de prácticas
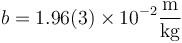
o
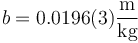
o
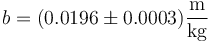
Cualquiera de estas tres formas es válida, aunque por las limitaciones de espacio, es preferible la forma compacta con la incertidumbre entre paréntesis.
5.6 Incertidumbre de la ordenada, Ea
La ordenada en el origen tiene también su propia incertidumbre, causada en este caso por tres factores:
- Por la incertidumbre de cada una de las medidas individuales
- Por el hecho de que se trata de una estimación estadística
- Por la incertidumbre en la pendiente. Este último factor influye en que según la pendiente sea un poco mayor o un poco menor, el punto de corte con el eje de ordenadas bajará o subirá.
La fórmula para el error en la ordenada en el origen es
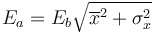
donde Eb es la incertidumbre de la pendiente (que hallamos antes), 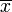 es el valor medio de las x (que en Excel se halla con la función PROMEDIO) y
es el valor medio de las x (que en Excel se halla con la función PROMEDIO) y 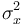 es la varianza de la población
es la varianza de la población
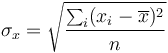
Esta cantidad se halla en Excel 2010 con la función VAR.P, (en Excel 2007 y anteriores con la función VAR; también funciona en Excel 2010). Con esto nos queda la orden
=F4*RAIZ(PROMEDIO(B3:B8)^2+VAR(B3:B8))
siendo F4 la celda donde está almacenada la incertidumbre de la pendiente.
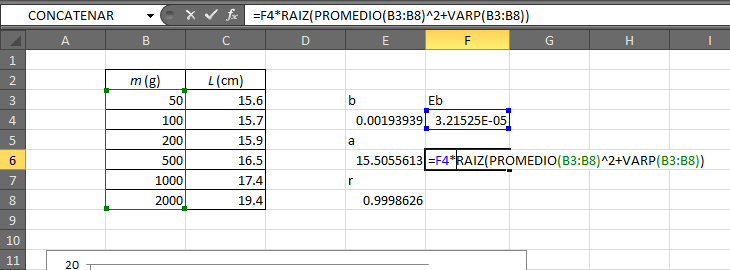
En nuestro ejemplo nos da un valor de 0.029579829. Teniendo en cuenta que la incertidumbre de la ordenada tiene las mismas unidades que ésta, sería
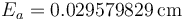
5.7 Expresión de la ordenada con su incertidumbre
Reuniendo el valor de a con el de su incertidumbre queda
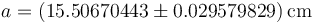
Ahora corresponde redondear empleando las mismas técnicas que para cualquier otra magnitud con incertidumbre. Escribimos el valor de la magnitud y el de su incertidumbre uno bajo el otro, alineando los puntos decimales
15.50670443 0.029579829
Consideramos las dos primeras cifras significativas de la incertidumbre (29). Al ser mayores que 25 se redondea a una sola cifra
15.50670443 0.03
Redondeamos la magnitud hasta la última cifra del error. Puesto que la siguiente cifra (6) es mayor que 5, redondeamos hacia arriba
15.51 0.03
Con esto nos queda el valor de la ordenada
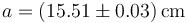
En forma compacta, escribiendo la incertidumbre entre paréntesis
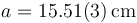
Pasamos este valor a las unidades fundamentales del sistema internacional
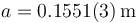
Esto es lo que tenemos que escribir en la casilla correspondiente del formulario. Alternativamente, podemos poner
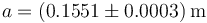
aunque por las limitaciones de espacio, es preferible la forma compacta.
5.8 Resumen de los pasos
Resumiendo, tenemos los siguientes pasos para hacer los cálculos de la recta de mejor ajuste
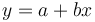
a una serie de datos (xi,yi)
- Se almacenan los datos en una tabla de dos columnas
- Se hace una gráfica de los puntos experimentales, para ver si hay alguno que descartar. Si lo hubiera, se borra de la tabla.
- Se calcula la pendiente, b.
- Se calcula la ordenada en el origen, a.
- Se halla el coeficiente de correlación, r. Se expresa hasta el primer número que no sea un 9 tras el punto decimal.
- Se calcula la incertidumbre de la pendiente, Eb (que requiere conocer b y r)
- Se expresa la pendiente con su incertidumbre, redondeando donde sea preciso y colocando las unidades adecuadas.
- Se halla la incertidumbre de la ordenada, Ea (precisa de Eb)
- Se expresa la ordenada en el origen con su incertidumbre, redondeando donde sea preciso y colocando las unidades adecuadas.
Detalles a tener en cuenta:
- b es la pendiente y a es la ordenada en el origen; en algunas calculadoras y textos de referencia, se usa la notación inversa, por lo que hay que tener mucho cuidado.
- La pendiente tiene unidades, las de “y” divididas por las de “x”. Es un error muy grave escribir la pendiente sin unidades porque “es un número que da la calculadora (o Excel)”. En general, convendrá pasar a las unidades fundamentales del SI.
- La ordenada en el origen también tiene unidades, las de “y”. También está mal el cálculo si no se ponen.
- La regla de redondeo para r es diferente que para las otras dos cantidades.
6 Haciendo la gráfica
Una parte importante de todo cálculo de rectas de mejor ajuste es su representación gráfica. De hecho, en las prácticas de Física se entiende que siempre que se pida calcular una recta por mínimos cuadrados, hay que adjuntar la gráfica correspondiente.
El trazado de una gráfica tiene unas normas de presentación específicas, que hay que respetar. No puede uno limitarse a aceptar lo que produce Excel sin más. El objeto de una gráfica no es simplemente ilustrar un fenómeno. Se trata de una herramienta muy útil. Para ello, debe presentar toda la información necesaria de forma clara.
Veamos cómo se hace una buena gráfica en Excel.
6.1 La gráfica, lo más grande posible
El primer paso consiste en ampliar la gráfica para aumentar su visibilidad.
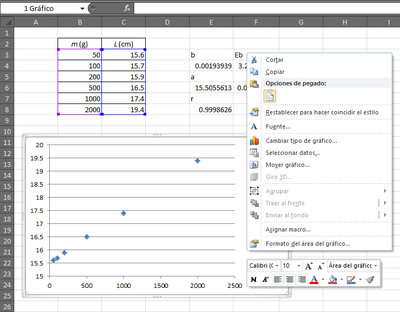
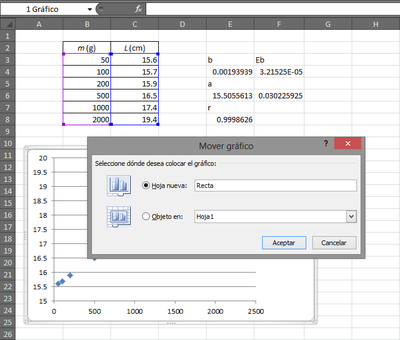
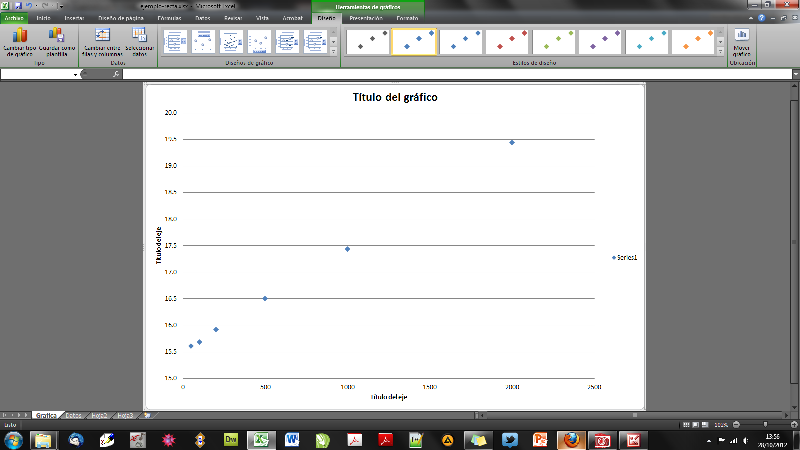
Recordemos que ya habíamos trazado una gráfica de los puntos experimentales. Para ampliarla la movemos a una hoja nueva. Pulsando con el botón de la derecha en una zona libre de la gráfica aparece un menú contextual. Mediante la opción "Mover gráfico" (o "Ubicación...") podemos elegir el cambiarlo de hoja. De este modo obtenemos una gráfica que ocupa toda una página
6.2 Cuadrícula en la gráfica
En una representación sobre papel milimetrado, la posición de los puntos se puede leer fácilmente a partir de su posición en la cuadrícula. En una gráfica producida por ordenador se aplica el mismo principio. Debe haber una cuadrícula que permita localizar de forma sencilla los valores aproximados de los datos experimentales, sin necesidad de indicar los valores numéricos explícitamente.
Excel incluye entre sus plantillas para los gráficos del tipo "Dispersión" o "XY" una

que prácticamente produce una gráfica con casi todas las propiedades que vamos a emplear.
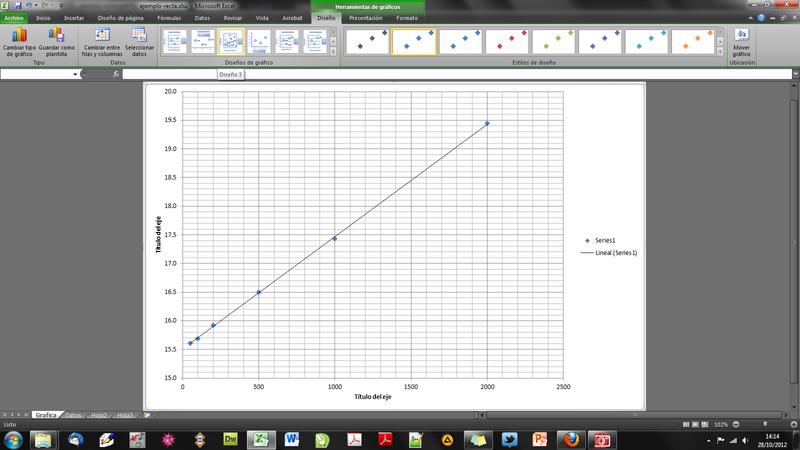
Suponiendo que no tenemos, o no sabemos emplear, esta plantilla, podemos fijar todos los parámetros manualmente a partir de la gráfica básica que teníamos antes.
6.2.1 Límites en los ejes
El primer paso para trazar la cuadrícula consiste en establecer los límites de los ejes. En una gráfica no hay ninguna obligación de que el punto (0,0) esté en la esquina. Por el contrario, lo más probable es que ni aparezca en la gráfica. Los límites de la gráfica se eligen tomando dos valores más o menos "redondos", uno de los cuales esté algo por debajo del menor dato y otro algo por encima del mayor.
En nuestro ejemplo, para la x, que va de 50 a 2000, toamos los límites 0 y 2000, y para la y, que va de 15.6 a 19.4 tomamos los límites en 15 y 20.
En Excel, para fijar los límites, marcamos en un número del eje que queremos modificar y elegimos la opción "Dar formato a eje...". En el formulario que aparece seleccionamos la opción de fijar manualmente los límites superior e inferior, así como las divisiones principales y secundarias (las principales corresponden a la cuadrícula gruesa y la secundaria a la fina).
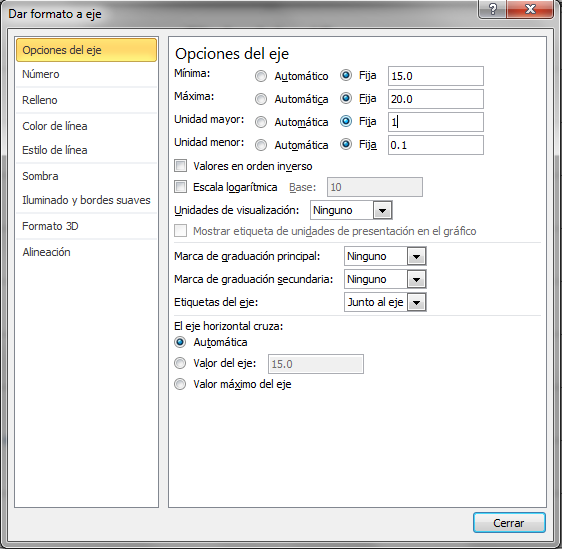
6.2.2 Trazado de la cuadrícula
A continuación, pulsando de nuevo en un número del eje, seleccionamos las opciones de "Agregar líneas de división principales" y "Agregar líneas de división secundarias".
Repetimos la operación con el otro eje y así obtenemos la gráfica cuadriculada.
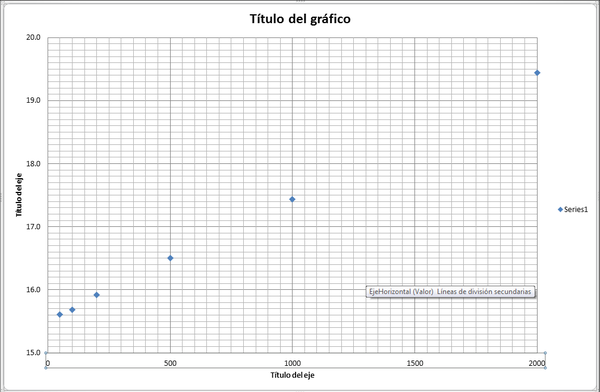
6.3 Etiquetas y título
Toda gráfica debe estar correctamente identificada.
- Debe tener un título descriptivo de qué se representa frente a qué.
- En cada eje debe aparecer el símbolo de la magnitud (el mismo que se emplee en las fórmulas) y la unidad de medida.
Para ello, editamos el título y las etiquetas, simplemente pinchando en ellas.
Si nuestra gráfica por defecto no trae ni título de gráfico ni rótulo de ejes, los insertamos yendo a la pestaña "Presentación" y pulsando en las opciones correspondientes
Con esto nos queda una gráfica correctamente rotulada.

6.4 Formato de los puntos
Los puntos experimentales deben ser claramente visibles. Por ello, no es conveniente un marcador (el símbolo usado para marcarlos), que sea un punto gordo, pues no deja clara la posición exacta del dato.
Por ello, debemos cambiar el formato de la serie de datos (pulsando con el botón derecho en uno de los puntos experimentales y eligiendo "Dar formato a serie de datos...") y elegir un marcador en forma de aspa o similar, que sea además de un color oscuro, para que se va bien al imprimirlo. Existen muchas opciones que pueden modificarse (color del marcador, grosor de sus líneas, tamaño del marcador, etc.)
Una opción debe evitarse siempre: No se debe trazar la línea quebrada que uniría los puntos. Puesto que no tenemos información sobre lo que pasa entre dato y dato, esta línea es superflua.
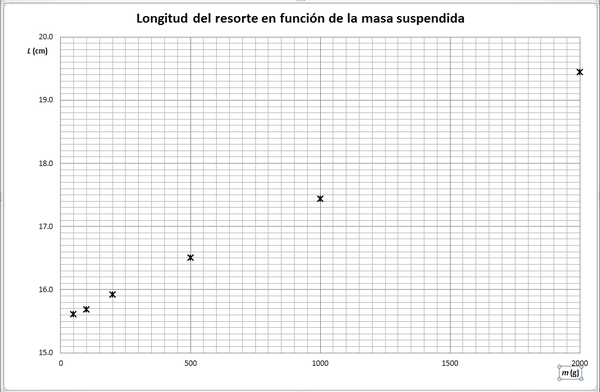
La etiqueta por defecto "Serie 1" que coloca Excel puede ser suprimida sin problemas.
6.5 Recta de mejor ajuste
Por último, queda trazar la recta de mejor ajuste. En principio, puede hacerse a partir de los datos de a y b hallados antes. Sin embargo, en Excel es mucho más sencillo: basta pulsar de nuevo en un punto experimental con el botón derecho del ratón y elegir la opción "Agregar línea de tendencia...". Se abre entonces un menú de opciones que nos permiten elegir el tipo de ajuste (lineal, en la práctica totalidad de los casos), el color de la línea, su grosor, etc.
La recta de mejor ajuste debe ser claramente visible y debe dejar ver los marcadores de los puntos experimentales, por lo que hay que buscar que su color sea diferente y que los marcadores sobresalgan claramente de la línea.
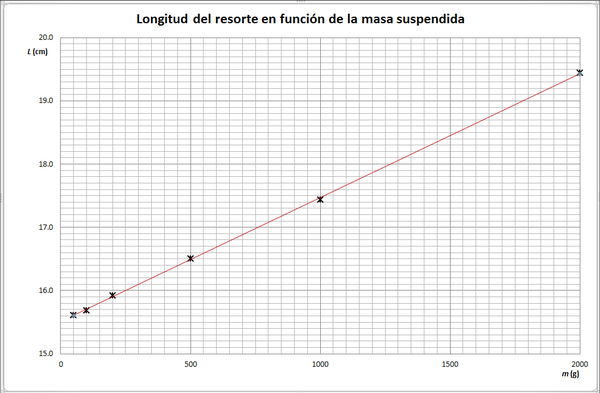
Aparte de todo esto, pueden afinarse multitud de pequeños detalles como tamaño de los rótulos, fuentes de texto, colores y grosores de las líneas de división, etc.





