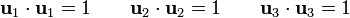Base ortonormal dextrógira
De Laplace
(Diferencias entre revisiones)
Gonfer (Discusión | contribuciones)
(Nueva página: ==Definición== Una base vectorial se dice que es ortonormal dextrógira, si sus vectores son unitarios, ortogonales, y verifican la regla de la mano derecha. ==Vectores unitarios==...)
Edición más nueva →
(Nueva página: ==Definición== Una base vectorial se dice que es ortonormal dextrógira, si sus vectores son unitarios, ortogonales, y verifican la regla de la mano derecha. ==Vectores unitarios==...)
Edición más nueva →
Revisión de 16:58 21 nov 2007
1 Definición
Una base vectorial se dice que es ortonormal dextrógira, si sus vectores son unitarios, ortogonales, y verifican la regla de la mano derecha.
2 Vectores unitarios
Un vector es unitario cuando su módulo es la unidad. Matemáticamente, esto quiere decir que si la base vectorial es No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \left{\mathbf{u}_1,\mathbf{u}_2,\mathbf{u}_3\}
se cumple