Entrar Página Discusión Historial Go to the site toolbox

Cálculo de circulación

De Laplace

(Diferencias entre revisiones)
(→Circunferencia vertical)
(→Circunferencia vertical)
Línea 67: Línea 67:
En cada una de ellas
En cada una de ellas
-
<center><math>\mathbf{A} = R\mathbf{u}_{r}+R\sen\theta\,\mathbf{u}_{\varphi}</math>{{qquad}}{{qquad}}<math>\mathrm{d}\mathbf{r} = R\,\mathrm{d}\theta\,\mathbf{u}_{\theta}</math></center>
+
<center><math>\mathbf{A} = R\mathbf{u}_{r}+R\,\mathrm{sen}\,\theta\,\mathbf{u}_{\varphi}</math>{{qquad}}{{qquad}}<math>\mathrm{d}\mathbf{r} = R\,\mathrm{d}\theta\,\mathbf{u}_{\theta}</math></center>
y la circulación es
y la circulación es
Línea 75: Línea 75:
Por el teorema de Stokes, si queremos aplicar coordenadas esféricas, el rotacional vale
Por el teorema de Stokes, si queremos aplicar coordenadas esféricas, el rotacional vale
-
<center><math>\nabla\times\mathbf{A} = 2\mathbf{u}_{z} = 2\left(\cos\theta\mathbf{u}_{r}-\sen\theta\mathbf{u}_{\theta}\right)</math></center>
+
<center><math>\nabla\times\mathbf{A} = 2\mathbf{u}_{z} = 2\left(\cos\theta\mathbf{u}_{r}-\mathrm{sen}\,\theta\mathbf{u}_{\theta}\right)</math></center>
Para el diferencial de superficie, si consideramos el círculo delimitado por esta circunferencia resulta la unión de dos superficies
Para el diferencial de superficie, si consideramos el círculo delimitado por esta circunferencia resulta la unión de dos superficies

Revisión de 09:48 3 oct 2008

Contenido

1 Enunciado

Para el campo vectorial

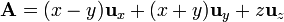
\mathbf{A} = (x-y)\mathbf{u}_{x}+(x+y)\mathbf{u}_{y}+z\mathbf{u}_{z}

calcule su circulación a lo largo de las siguientes curvas cerradas:

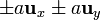  1. Un cuadrado de lado 2a, con vértices \pm a\mathbf{u}_{x}\pm a\mathbf{u}_{y}.
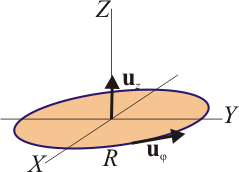
  2. Una circunferencia de radio R situada en el plano z = 0 y con centro el origen de coordenadas.
  3. Una circunferencia vertical, situada en el plano x = y y con centro el origen de coordenadas.

En cada caso, halle la circulación por integración directa y por aplicación del teorema de Stokes.

2 Solución

2.1 Cuadrado

La circulación a lo largo del cuadrado se compone de cuatro tramos, que calculamos por separado:

2.1.1 Primer Lado

Para el lado situado en x = a, z = 0,

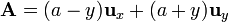
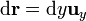
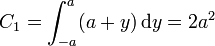
\mathbf{A} = (a-y)\mathbf{u}_{x}+(a+y)\mathbf{u}_{y}        \mathrm{d}{\mathbf{r}}=\mathrm{d}{y}\mathbf{u}_{y}   \Rightarrow   C_1 = \int_{-a}^a (a+y)\,\mathrm{d}{y} = 2a^2

2.1.2 Segundo lado

Para el situado en y = a, z = 0

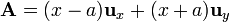
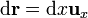
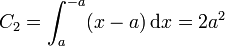
\mathbf{A} = (x-a)\mathbf{u}_{x}+(x+a)\mathbf{u}_{y}        \mathrm{d}{\mathbf{r}}=\mathrm{d}{x}\mathbf{u}_{x}   \Rightarrow   C_2 = \int_{a}^{-a} (x-a)\,\mathrm{d}{x} = 2a^2

Nótese que no hace falta cambiar el signo a 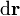\mathrm{d}{\mathbf{r}}, ya que el sentido de recorrido lo dan los límites de integración.

2.1.3 Tercer lado

Para el lado situado en x = − a, z = 0,

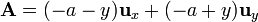
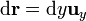
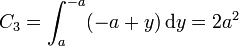
\mathbf{A} = (-a-y)\mathbf{u}_{x}+(-a+y)\mathbf{u}_{y}        \mathrm{d}{\mathbf{r}}=\mathrm{d}{y}\mathbf{u}_{y}   \Rightarrow   C_3 = \int_{a}^{-a} (-a+y)\,\mathrm{d}{y} = 2a^2

2.1.4 Cuarto lado

Para el situado en y = − a, z = 0

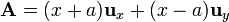
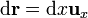
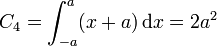
\mathbf{A} = (x+a)\mathbf{u}_{x}+(x-a)\mathbf{u}_{y}        \mathrm{d}{\mathbf{r}}=\mathrm{d}{x}\mathbf{u}_{x}   \Rightarrow   C_4 = \int_{-a}^{a} (x+a)\,\mathrm{d}{x} = 2a^2

2.1.5 Circulación

Sumando las cuatro contribuciones

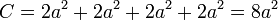
C = 2a^2+2a^2+2a^2+2a^2 = 8a^2\,

2.1.6 Aplicación del teorema de Stokes

Empleando el teorema de Stokes tenemos

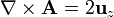
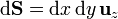
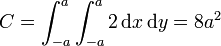
\nabla\times\mathbf{A} = 2\mathbf{u}_{z}        \mathrm{d}{\mathbf{S}} = \mathrm{d}{x}\,\mathrm{d}{y}\,\mathbf{u}_{z}   \Rightarrow   C = \int_{-a}^a\int_{-a}^a 2\,\mathrm{d}{x}\,\mathrm{d}{y} = 8a^2

2.2 Circunferencia horizontal

Para el caso de la circunferencia horizontal centrada en el origen, empleamos coordenadas cilíndricas, en las cuales esta circunferencia es una línea coordenada de \varphi, con ρ = R, z = 0. De esta forma
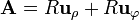
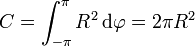
\mathbf{A} = R\mathbf{u}_{\rho}+R\mathbf{u}_{\varphi}        \mathrm{d}\mathbf{r} = R\,\mathrm{d}\varphi\,\mathbf{u}_{\varphi}   \Rightarrow   C = \int_{-\pi}^\pi R^2\,\mathrm{d}\varphi = 2\pi R^2

Esta misma circulación, mediante el teorema de Stokes sería

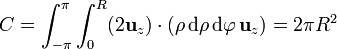
C = \int_{-\pi}^\pi\int_0^R (2\mathbf{u}_{z})\cdot \left(\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi\,\mathbf{u}_{z}\right) = 2\pi R^2

donde hemos tomado como superficie de integración el círculo apoyado en la circunferencia en la que queremos hallar la circulación.

2.3 Circunferencia vertical

Para la circunferencia vertical empleamos coordenadas esféricas, ya que esta circunferencia está compuesta por dos líneas coordenadas de θ por tratarse de dos meridianos unidos. Estas dos líneas son
\varphi = \frac{\pi}{4}\qquad r = R        y        \varphi = -\frac{3\pi}{4}\qquad r = R

En cada una de ellas

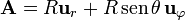
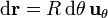
\mathbf{A} = R\mathbf{u}_{r}+R\,\mathrm{sen}\,\theta\,\mathbf{u}_{\varphi}        \mathrm{d}\mathbf{r} = R\,\mathrm{d}\theta\,\mathbf{u}_{\theta}

y la circulación es

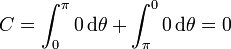
C = \int_0^\pi 0\,\mathrm{d}\theta + \int_\pi^0 0\,\mathrm{d}\theta = 0

Por el teorema de Stokes, si queremos aplicar coordenadas esféricas, el rotacional vale

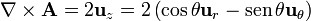
\nabla\times\mathbf{A} = 2\mathbf{u}_{z} = 2\left(\cos\theta\mathbf{u}_{r}-\mathrm{sen}\,\theta\mathbf{u}_{\theta}\right)

Para el diferencial de superficie, si consideramos el círculo delimitado por esta circunferencia resulta la unión de dos superficies 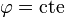\varphi=\mathrm{cte} (cada una un semicírculo), resulta

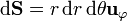
\mathrm{d}\mathbf{S} = r\,\mathrm{d}{r}\,\mathrm{d}{\theta}\mathbf{u}_{\varphi}

por lo que

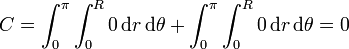
C = \int_0^\pi \int_0^R 0\,\mathrm{d}{r}\,\mathrm{d}{\theta} + \int_0^\pi \int_0^R 0\,\mathrm{d}{r}\,\mathrm{d}{\theta} = 0

Gráficamente es evidente que la circulación se anula pues el rotacional va en la dirección del eje Z, mientras que el vector 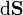\mathrm{d}\mathbf{S} va en una dirección horizontal.

Obtenido de "http://tesla.us.es/wiki/index.php/C%C3%A1lculo_de_circulaci%C3%B3n"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace