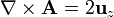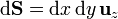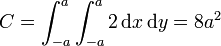Cálculo de circulación
De Laplace
(Diferencias entre revisiones)
(→Tercer lado) |
(→Cuarto lado) |
||
| Línea 36: | Línea 36: | ||
Para el situado en <math>y=-a</math>, <math>z=0</math> | Para el situado en <math>y=-a</math>, <math>z=0</math> | ||
| - | <center><math>\mathbf{A} = (x+a)\mathbf{u}_{x}+(x-a)\mathbf{u}_{y}</math>{{qquad}}{{qquad}} | + | <center><math>\mathbf{A} = (x+a)\mathbf{u}_{x}+(x-a)\mathbf{u}_{y}</math>{{qquad}}{{qquad}}<math>\mathrm{d}{\mathbf{r}}=\mathrm{d}{x}\mathbf{u}_{x}</math>{{tose}}<math>C_4 = \int_{-a}^{a} (x+a)\,\mathrm{d}{x} = 2a^2</math></center> |
| - | <math>\mathrm{d}{\mathbf{r}}=\mathrm{d}{x}\mathbf{u}_{x}</math>{{tose}} | + | |
| - | <math>C_4 = \int_{-a}^{a} (x+a)\,\mathrm{d}{x} = 2a^2</math></center> | + | |
====Circulación==== | ====Circulación==== | ||
Revisión de 08:26 3 oct 2008
Contenido |
1 Enunciado
Para el campo vectorial
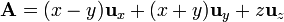
calcule su circulación a lo largo de las siguientes curvas cerradas:
- Un cuadrado de lado 2a, con vértices
.
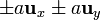- Una circunferencia de radio R situada en el plano z = 0 y con centro el origen de coordenadas.
- Una circunferencia vertical, situada en el plano x = y y con centro el origen de coordenadas.
En cada caso, halle la circulación por integración directa y por aplicación del teorema de Stokes.
2 Solución
2.1 Cuadrado
La circulación a lo largo del cuadrado se compone de cuatro tramos, que calculamos por separado:
2.1.1 Primer Lado
Para el lado situado en x = a, z = 0,
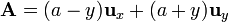
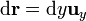
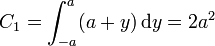
2.1.2 Segundo lado
Para el situado en y = a, z = 0
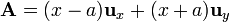
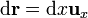
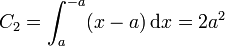
Nótese que no hace falta cambiar el signo a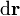 
, ya que el sentido de recorrido lo dan los límites de integración.
2.1.3 Tercer lado
Para el lado situado en x = − a, z = 0,
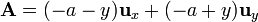
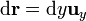
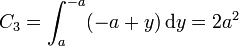
2.1.4 Cuarto lado
Para el situado en y = − a, z = 0
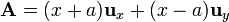
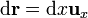
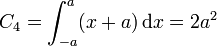
2.1.5 Circulación
Sumando las cuatro contribuciones
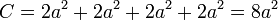
2.1.6 Aplicación del teorema de Stokes
Empleando el teorema de Stokes tenemos
