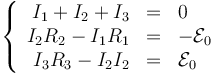Barra resistiva deslizante
De Laplace
(Página creada con '==Enunciado== Tres barras de longitud <math>a</math> con resistencias <math>R_1</math>, <math>R_2</math> y <math>R_3</math> se encuentran conectadas por raíles perfectamente co…') |
|||
| Línea 8: | Línea 8: | ||
==Corrientes y voltajes== | ==Corrientes y voltajes== | ||
| + | Tenemos un circuito formado por dos mallas. La fuerza electromotriz en cada una la obtenemos aplicando la ley de Faraday | ||
| + | |||
| + | <center><math>\mathcal{E}=-\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | Consideramos para cada malla un sentido de recorrido antihorario, de forma que el flujo magnético sea positivo en ambas. | ||
| + | |||
| + | En la de la izquierda tenemos | ||
| + | |||
| + | <center><math>\Phi_1 = B_0ax\qquad\Rightarrow\qquad \mathcal{E}_1 = -\frac{\mathrm{d}\Phi_1}{\mathrm{d}t}=-B_0a v_0</math></center> | ||
| + | |||
| + | y en la de la derecha | ||
| + | |||
| + | <center><math>\Phi_2 = B_0a(b-x)\qquad\Rightarrow\qquad \mathcal{E}_2 = -\frac{\mathrm{d}\Phi_2}{\mathrm{d}t}=+B_0a v_0</math></center> | ||
| + | |||
| + | Vemos que resultan fuerzas electromotrices de la misma magnitud pero signo opuesto. | ||
| + | |||
| + | <center><math>\mathcal{E}_1 = -\mathcal{E}_0\qquad\qquad\mathcal{E}_2 = +\mathcal{E}_0</math></center> | ||
| + | |||
| + | Para hallar la corriente por las diferentes ramas, analizamos el circuito. Suponemos sentidos de la corriente hacia arriba en cada una de las resistencias. Esto implica, por la primera ley de Kirchhoff aplicada a los nodos | ||
| + | |||
| + | <center><math>I_1+I_2+I_3 = 0\,</math></center> | ||
| + | |||
| + | mientras que la segunda ley de Kirchhoff aplicada a la malla de la izquierda da | ||
| + | |||
| + | <center><math>I_2R_2-I_3R_3 = \mathcal{E}_1 = -\mathcal{E}_0</math></center> | ||
| + | |||
| + | y aplicada a la de la derecha | ||
| + | |||
| + | <center><math>I_3R_3-I_2R_2 = \mathcal{E}_2 = \mathcal{E}_0</math></center> | ||
| + | |||
| + | Tenemos entonces el sistema de ecuaciones | ||
| + | |||
| + | <center><math>\left\{\begin{array}{rcl} I_1+I_2+I_3 & = & 0 \\ I_2R_2-I_1R_1 & = & -\mathcal{E}_0 \\ I_3R_3-I_2I_2 & = & \mathcal{E}_0\end{array}\right.</math></center> | ||
| + | |||
| + | |||
==Potencia disipada== | ==Potencia disipada== | ||
==Fuerza y potencia mecánica== | ==Fuerza y potencia mecánica== | ||
Revisión de 22:16 9 sep 2012
Contenido |
1 Enunciado
Tres barras de longitud a con resistencias R1, R2 y R3 se encuentran conectadas por raíles perfectamente conductores (ver figura). La barra 1 y la 3 están en reposo, separadas una distancia b, pero la 2 se mueve hacia la derecha con velocidad v0, siendo su distancia a la primera barra una cantidad x(t). Todo el sistema se encuentra sumergido en un campo magnético uniforme 
perpendicular al circuito.
- Calcule la corriente que circula por cada barra, así como el voltaje entre los extremos de cada una de ellas.
- Calcule la potencia disipada en el circuito por efecto Joule.
- Halle la fuerza que el campo magnético ejerce sobre la barra central. ¿Qué potencia desarrolla esta fuerza?
- Considere el caso en el que la resistencia 1 es un amperímetro (
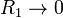) y la 3 un voltímetro (
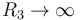). ¿Qué corriente marca el amperímetro y que voltaje el voltímetro?
2 Corrientes y voltajes
Tenemos un circuito formado por dos mallas. La fuerza electromotriz en cada una la obtenemos aplicando la ley de Faraday
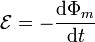
Consideramos para cada malla un sentido de recorrido antihorario, de forma que el flujo magnético sea positivo en ambas.
En la de la izquierda tenemos
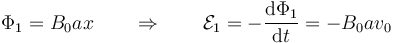
y en la de la derecha
Vemos que resultan fuerzas electromotrices de la misma magnitud pero signo opuesto.
Para hallar la corriente por las diferentes ramas, analizamos el circuito. Suponemos sentidos de la corriente hacia arriba en cada una de las resistencias. Esto implica, por la primera ley de Kirchhoff aplicada a los nodos
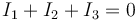
mientras que la segunda ley de Kirchhoff aplicada a la malla de la izquierda da
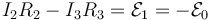
y aplicada a la de la derecha
Tenemos entonces el sistema de ecuaciones
