Diferencial de una función
De Laplace
(Diferencias entre revisiones)
(→Propiedades de los diferenciales) |
(→Concepto) |
||
| Línea 1: | Línea 1: | ||
==Concepto== | ==Concepto== | ||
| + | En la definición de [[derivada direccional]] (y en la derivada ordinaria) aparece el límite de un cociente de incrementos | ||
| + | |||
| + | <center><math>\frac{\partial\phi}{\partial v} = \lim_{|\Delta\mathbf{r}|\to 0}\frac{\Delta\phi}{|\Delta\mathbf{r}|}</math></center> | ||
| + | |||
| + | que se puede escribir como el cociente de dos cantidades infinitesimales: | ||
| + | |||
| + | <center><math> \lim_{|\Delta\mathbf{r}|\to 0}\frac{\Delta\phi}{|\Delta\mathbf{r}|}=\frac{\mathrm{d}\phi}{|\mathrm{d}\|mathbf{r}|}</math></center> | ||
| + | |||
| + | El denominador, <math>|\mathrm{d}\mathbf{r}|</math> es una distancia infinitesimal, modulo de vector desplazamiento diferencial. | ||
| + | |||
| + | El numerador, <math>\mathrm{d}\phi\,</math> es el diferencial de la función <math>\phi\,</math>, definido como el incremento infinitesimal entre dos puntos vecinos: | ||
| + | |||
| + | <center><math>\mathrm{d}\phi = \phi\left(\mathbf{r}+\mathrm{d}\mathbf{r}\right)-\phi\left(\mathbf{r}\right)</math></center> | ||
| + | |||
==Diferencial ≠ derivada== | ==Diferencial ≠ derivada== | ||
==Propiedades de los diferenciales== | ==Propiedades de los diferenciales== | ||
[[Categoría:Gradiente]] | [[Categoría:Gradiente]] | ||
Revisión de 09:24 2 oct 2008
1 Concepto
En la definición de derivada direccional (y en la derivada ordinaria) aparece el límite de un cociente de incrementos
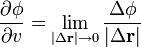
que se puede escribir como el cociente de dos cantidades infinitesimales:

El denominador, 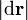 es una distancia infinitesimal, modulo de vector desplazamiento diferencial.
es una distancia infinitesimal, modulo de vector desplazamiento diferencial.
El numerador, 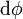 es el diferencial de la función
es el diferencial de la función  , definido como el incremento infinitesimal entre dos puntos vecinos:
, definido como el incremento infinitesimal entre dos puntos vecinos:






