Dilatación de un puente

De Laplace

(Diferencias entre revisiones)

última version al 10:35 6 jun 2012

1 Enunciado

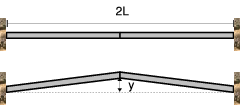
Se colocan dos tramos prefabricados de hormigón en un puente de longitud total $2 L$ , de modo que no queda espacio para una posible dilatación. Si se produce un aumento de temperatura $Δ T$ , ¿cuánto mide la altura $y$ a la que se levantan ambos tramos al deformarse?

2 Solución

Al aumentar la temperatura una cantidad $Δ T$ , la longitud de cada tramo aumenta hasta

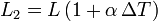
$L_2 = L\,(1+\alpha\,\Delta T)$

Aquí $α$ es el coeficiente medio de dilatación lineal del hormigón. La altura $y$ se obtiene aplicando el teorema de Pitágoras

$y = \left[ L^2-L_2^2\right]^{1/2}= L\left[1-(1+\alpha\,\Delta T)^2\right]^{1/2}= L\left[2\alpha\,\Delta T + \alpha^2(\Delta T)^2\right]^{1/2}$

Teniendo en cuenta que 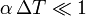$\alpha\,\Delta T\ll 1$

$y=L\left(2\alpha\,\Delta T\right)^{1/2} \left[1 + \dfrac{1}{2}\alpha\,\Delta T\right]^{1/2}$

Usando el desarrollo de Taylor

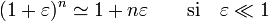
$(1+\varepsilon)^n\simeq 1+ n\varepsilon \qquad \mathrm{si}\quad\varepsilon\ll 1$

Tenemos

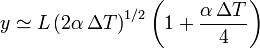
$y\simeq L\left(2\alpha\,\Delta T\right)^{1/2} \left(1+\dfrac{\alpha\,\Delta T}{4}\right)$

Podemos despreciar el segundo sumando del paréntesis, con lo cual

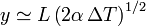
$y\simeq L\left(2\alpha\,\Delta T\right)^{1/2}$

Según las tablas 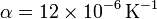$\alpha=12\times10^{-6}\,\mathrm{K^{-1}}$ Si suponemos un tramo de 50 m y una diferencia de temperatura entre invierno y verano de 50 ^oC tenemos

$y\simeq 1.73\,\mathrm{m}$

@@ Línea 52: / Línea 52: @@
 </math>
 </center>
-[[Categoría:Problemas de temperatura|0]]
+[[Categoría:Problemas de temperatura y Principio 0 F2 GIA]]
-[[Categoría:Temperatura y Principio cero]]

Dilatación de un puente

De Laplace

última version al 10:35 6 jun 2012

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES