Campo eléctrico y ley de Gauss (GIE)
De Laplace
(→Líneas de campo eléctrico) |
|||
| Línea 40: | Línea 40: | ||
* Un campo central | * Un campo central | ||
| - | <center><math>\vec{E}(\vec{r}) = E(r)\vec{u}_r\qquad \qquad (\mbox{campo central | + | <center><math>\vec{E}(\vec{r}) = E(r)\vec{u}_r\qquad \qquad (\mbox{campo central})</math></center> |
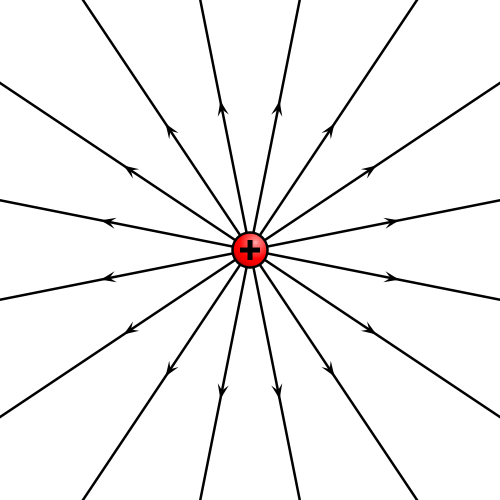
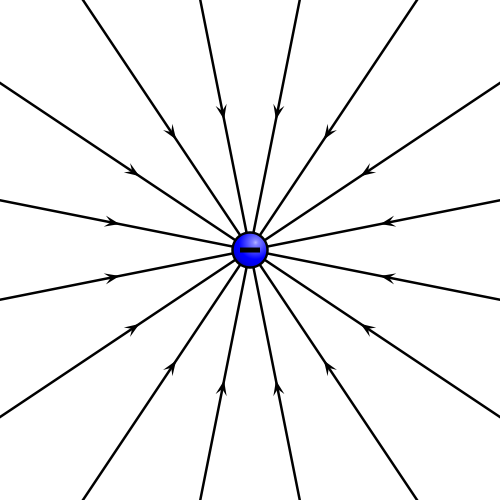
:en el cual el campo es siempre puramente radial, las líneas de campo son semirrectas radiales. Este es el caso del campo de una carga puntual, positiva o negativa, ilustrados arriba. | :en el cual el campo es siempre puramente radial, las líneas de campo son semirrectas radiales. Este es el caso del campo de una carga puntual, positiva o negativa, ilustrados arriba. | ||
| + | |||
==Ley de Gauss== | ==Ley de Gauss== | ||
==Campo de cargas puntuales== | ==Campo de cargas puntuales== | ||
Revisión de 08:45 26 may 2012
Contenido |
1 Concepto de electrostática
La electrostática estudia los campos eléctricos y fuerzas debidas a cargas en reposo. Si además es “en el vacío” queiere decir que se consideran las cargas flotando en un espacio vacío. Puesto que más del 99% de la materia es realmente vacío, es un punto de partida adecuado. Los medios materiales (conductores o dieléctricos) pueden añadirse más tarde, como conjunto de cargas en el vacío.
En la electrostática en el vacío, los campos eléctricos son independientes dle tiempo y no hay campos magnéticos presentes. Esto reduce la ley de Lorentz para una carga puntual a solo la fuerza eléctrica
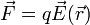
y puesto que consideramos cargas en reposo suponemos que esta fuerza se encuentra compensada por alguna otra, de forma que la resultante es nula.
2 Campo eléctrico
Entendemos el campo eléctrostático como una perturbación en el espacio producida por la presencia de cargas eléctricas en reposo
| 
|
| 
|
El campo es un concepto primario. No se puede describir qué es el campo eléctrico, sino solo qué efectos produce sobre otras cargas.
Puede definirse de una manera operativa, esto es, dando un procedimiento para su medida. Para ello se considera una carga muy pequeña q0 y se sitúa en un campo eléctrico. Con la medida de un dinamómetro se mide la fuerza sobre ella. Se define el campo eléctrico en la posición de la carga como
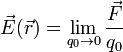
El límite se toma porque idealmente se considera que la carga que se coloca no debe afectar a lo que ya había, para lo cual debe ser lo más pequeña posible.
3 Líneas de campo eléctrico
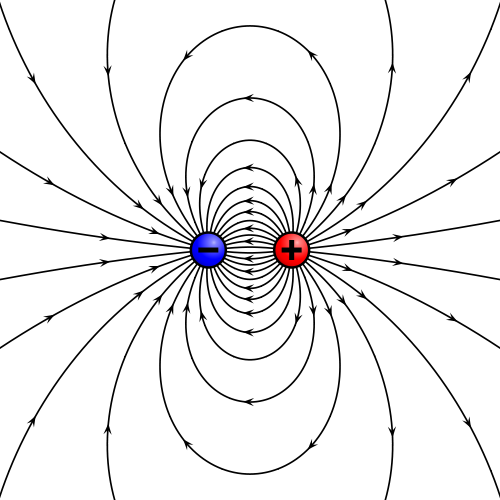
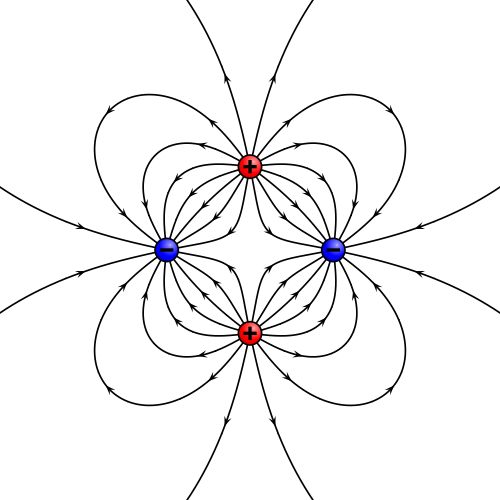
Como con cualquier otro campo, se pueden trazar las líneas de campo eléctrico, como aquellas curvas que son tangentes al campo eléctrico en cada punto. Estas curvas son soluciones de la ecuación diferencial
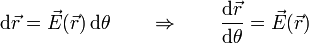
siendo θ un parámetro que nos permite etiquetar los puntos de cada curva. Estas ecuaciones diferenciales suelen ser extremadamente complejas y no poseen soluciones analíticas salvo en los casos más triviales, por lo que su solución requiere el uso de ordenadores, como en el caso de las cuatro cargas representado más arriba.
Existe casos particulares importantes:
- Un campo uniforme (independiente de la posición) tiene líneas de campo que son rectas paralelas
- Un campo central

- en el cual el campo es siempre puramente radial, las líneas de campo son semirrectas radiales. Este es el caso del campo de una carga puntual, positiva o negativa, ilustrados arriba.





