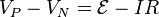Condensador con pérdidas
De Laplace
| Línea 33: | Línea 33: | ||
<center><math>Q = C\,\Delta V = C\mathcal{E}\qquad \qquad C = \frac{\varepsilon\mathcal{E}}{S}</math></center> | <center><math>Q = C\,\Delta V = C\mathcal{E}\qquad \qquad C = \frac{\varepsilon\mathcal{E}}{S}</math></center> | ||
| + | |||
| + | El que haya corriente se explica porque las cargas positivas de una placa atraen a las negativas de la otra y en este caso pueden fluir por el material intermedio. Si las placas no se descargan es porque la fuente de tensión va reponiendo de forma continua las cargas que escapan. Esto quiere decir que aunque la carga del condensador permanece constante, las cargas individuales van siendo sustituidas sucesivamente. | ||
| + | |||
==Energía y potencia== | ==Energía y potencia== | ||
| + | En este sistema existe una energía almacenada que puede calcularse a partir del campo eléctrico | ||
| + | |||
| + | <center><math>U_\mathrm{e}=\frac{1}{2}\int\varepsilon E^2\,\mathrm{d}v = \frac{1}{2}\left(\frac{\mathcal{E}}{a}\right)^2 a S = \frac{1}{2}C(\Delta V)^2</math></center> | ||
| + | |||
| + | Al mismo tiempo, se está disipando energía a un ritmo constante, por efecto Joule | ||
| + | |||
| + | <center><math>P = \frac{(\Delta V)^2}{R}= \frac{\mathcal{E}^2}{R}</math></center> | ||
| + | |||
| + | Esto quiere decir que para mantener el condensador cargado, la fuente debe suministrar carga y energía de forma continua. | ||
| + | |||
==Circuito equivalente== | ==Circuito equivalente== | ||
| + | Este elemento es tanto un condensador (caracterizado por una carga y una energía almacenadas), de capacidad <math>C</math>, como una resistencia <math>R</math> (caracterizada por una corriente y una potencia disipada por efecto Joule). La diferencia de potencial entre los extremos de la resistencia es la misma que entre los del condensador, por lo que ambos elementos están en paralelo. | ||
| + | |||
| + | Por ello, el circuito equivalente a un condensador real con pérdidas es una asociación en paralelo de un condensador y una resistencia, ambos ideales (es decir, el condensador ideal sin resistencia, y la resistencia sin capacidad). | ||
| + | |||
==Fuente real== | ==Fuente real== | ||
| + | Si la fuente conectada a las placas es una fuente real, entonces ya la diferencia de potencial ya no coincide con la fuerza electromotriz, sino que | ||
| + | |||
| + | <center><math>V_P-V_N = \mathcal{E}-IR\,</math></center> | ||
==Voltaje variable== | ==Voltaje variable== | ||
==Desconexión de la fuente== | ==Desconexión de la fuente== | ||
[[Categoría:Problemas de corriente eléctrica (GIE)]] | [[Categoría:Problemas de corriente eléctrica (GIE)]] | ||
Revisión de 14:51 23 may 2012
Contenido |
1 Enunciado
En un modelo de condensador real (“con pérdidas”) se tienen dos placas paralelas perfectamente conductoras de sección S, separadas una distancia a entre las cuales hay un dieléctrico de permitividad 
y con una pequeña conductividad σ. Entre las placas se establece una d.d.p. constante por medio de una fuente de f.e.m 
.
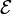- Calcule el campo eléctrico y la densidad de corriente entre las placas.
- Halle la energía almacenada en el sistema y la potencia consumida en el dispositivo.
- Diseñe el circuito equivalente a este dispositivo.
- Si la fuente que alimenta a este elemento es una fuente real con f.e.m. 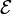y resistencia interna r, ¿cuánto valen en ese caso la carga, la corriente, la energía y la potencia?
- Si la d.d.p. que se aplica entre las placas no es continua, sino que varía como V(t), ¿qué corriente llega por el cable al dispositivo?
- ¿Qué ocurre si se desconecta la fuente?
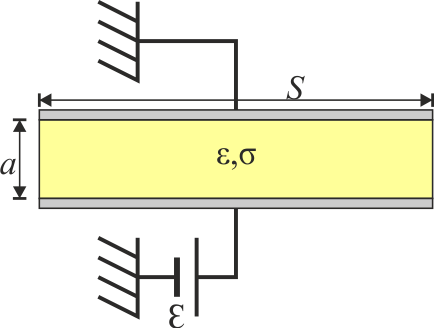
2 Campo y densidad de corriente
Al tratarse de un medio homogéneo situado entre dos placas paralelas, el campo eléctrico es uniforme en todo el material y proporcional a la diferencia de potencial
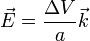
siendo 
el unitario que va en la dirección de la placa positiva a la negativa.
Si la fuente es ideal, la d.d.p. coincide con la fuerza electromotriz y
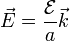
En el medio material existe una densidad de corriente proporcional al campo, según la ley de Ohm
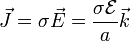
Esto quiere decir que el medio dieléctrico, al no ser perfectamente aislante, es atravesado por una intensidad de corriente
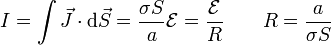
El que haya una corriente no quiere decir que las placas estén descargadas. Como en cualquier condensador plano habrá una carga
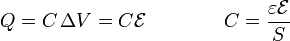
El que haya corriente se explica porque las cargas positivas de una placa atraen a las negativas de la otra y en este caso pueden fluir por el material intermedio. Si las placas no se descargan es porque la fuente de tensión va reponiendo de forma continua las cargas que escapan. Esto quiere decir que aunque la carga del condensador permanece constante, las cargas individuales van siendo sustituidas sucesivamente.
3 Energía y potencia
En este sistema existe una energía almacenada que puede calcularse a partir del campo eléctrico
Al mismo tiempo, se está disipando energía a un ritmo constante, por efecto Joule
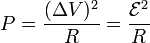
Esto quiere decir que para mantener el condensador cargado, la fuente debe suministrar carga y energía de forma continua.
4 Circuito equivalente
Este elemento es tanto un condensador (caracterizado por una carga y una energía almacenadas), de capacidad C, como una resistencia R (caracterizada por una corriente y una potencia disipada por efecto Joule). La diferencia de potencial entre los extremos de la resistencia es la misma que entre los del condensador, por lo que ambos elementos están en paralelo.
Por ello, el circuito equivalente a un condensador real con pérdidas es una asociación en paralelo de un condensador y una resistencia, ambos ideales (es decir, el condensador ideal sin resistencia, y la resistencia sin capacidad).
5 Fuente real
Si la fuente conectada a las placas es una fuente real, entonces ya la diferencia de potencial ya no coincide con la fuerza electromotriz, sino que
