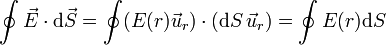Campo de distribuciones con simetría esférica
De Laplace
(Página creada con '==Enunciado== Con ayuda de la ley de Gauss, calcule el campo eléctrico en todos los puntos del espacio para las siguientes distribuciones con simetría esférica: # Una superf…') |
|||
| Línea 2: | Línea 2: | ||
Con ayuda de la ley de Gauss, calcule el campo eléctrico en todos los puntos del espacio para las siguientes distribuciones con simetría esférica: | Con ayuda de la ley de Gauss, calcule el campo eléctrico en todos los puntos del espacio para las siguientes distribuciones con simetría esférica: | ||
| + | # Una carga puntual <math>q</math>. | ||
# Una superficie esférica de radio <math>a</math> que almacena una carga <math>Q</math> distribuida uniformemente. | # Una superficie esférica de radio <math>a</math> que almacena una carga <math>Q</math> distribuida uniformemente. | ||
# Dos superficies esféricas concéntricas, de radios <math>a</math> y <math>b</math> (<math>a<b</math>) que almacenan respectivamente cargas <math>+Q</math> y <math>-Q</math>, distribuidas uniformemente. | # Dos superficies esféricas concéntricas, de radios <math>a</math> y <math>b</math> (<math>a<b</math>) que almacenan respectivamente cargas <math>+Q</math> y <math>-Q</math>, distribuidas uniformemente. | ||
| Línea 12: | Línea 13: | ||
==Introducción== | ==Introducción== | ||
| + | La ley de Gauss establece que el flujo del campo eléctrico a través de una superficie cerrada es proporcional a la carga encerrada en su interior | ||
| + | |||
| + | <center><math>\oint \vec{E}\cdot\mathrm{d}\vec{S}=\frac{Q_\mathrm{int}}{\varepsilon_0}</math></center> | ||
| + | |||
| + | siendo <math>\varepsilon_0</math> una constante universal conocida como ''permitividad del vacío''. | ||
| + | |||
| + | La ley de Gauss, aunque siempre es cierta, no siempre es útil como herramienta para hallar el campo eléctrico. La razón es que del valor de una integral definida no se deduce el valor del integrando (existen infinitas funciones diferentes que tienen la misma integral definida en un dominio dado). | ||
| + | |||
| + | Existe un caso, no obstante, en que la ley de Gauss permite obtener el campo eléctrico. Si la distribución de carga posee simetría esférica o de revolución, de manera que se ve igual desde todas las direcciones, el campo eléctrico que produce va en la dirección radial y depende solo de la distancia al centro de la distribución | ||
| + | |||
| + | <center><math>\vec{E}(\vec{r})=E(r)\vec{u}_r</math></center> | ||
| + | |||
| + | Este es el caso, por ejemplo, de una carga puntual. | ||
| + | |||
| + | Hay que remarcar que no todas las distribuciones de carga en una esfera poseen simetría esférica. Por ejemplo, una esfera cargada positivamente en su hemisferio “norte” y negativamente en el “sur” no posee simetría esférica, ya que no todas las direcciones son equivalentes. No se ve lo mismo desde el norte que desde el sur o desde el ecuador. | ||
| + | |||
| + | Suponiendo que sí existe simetría esférica, el flujo del campo eléctrico a través de una superficie esférica puede hallarse explícitamente. Si toamos una superficie esférica de radio <math>r</math> concéntrica con la distribución, el diferencial de superficie, ortogonal a ésta, va en la dirección radial | ||
| + | |||
| + | <center><math>\mathrm{d}\vec{S}=\mathrm{d}S\,\vec{u}_r</math></center> | ||
| + | |||
| + | Por ello, el flujo se reduce a una integral de un escalar | ||
| + | |||
| + | <center><math>\oint \vec{E}\cdot\mathrm{d}\vec{S}=\oint (E(r)\vec{u}_r)\cdot(\mathrm{d}S\,\vec{u}_r)=\oint E(r)\mathrm{d}S</math></center> | ||
| + | ==Una carga puntual== | ||
==Una superficie esférica== | ==Una superficie esférica== | ||
==Dos superficies concéntricas con cargas opuestas== | ==Dos superficies concéntricas con cargas opuestas== | ||
Revisión de 12:48 26 abr 2012
Contenido |
1 Enunciado
Con ayuda de la ley de Gauss, calcule el campo eléctrico en todos los puntos del espacio para las siguientes distribuciones con simetría esférica:
- Una carga puntual q.
- Una superficie esférica de radio a que almacena una carga Q distribuida uniformemente.
- Dos superficies esféricas concéntricas, de radios a y b (a < b) que almacenan respectivamente cargas + Q y − Q, distribuidas uniformemente.
- Dos superficies esféricas concéntricas, de radios a y b (a < b) cargadas respectivamente con densidades superficiales uniformes + σ0 y − σ0.
- Una esfera maciza de radio R que almacena una carga Q distribuida uniformemente en su volumen.
- Una esfera maciza de radio R con una densidad de carga dependiente de la distancia al centro como
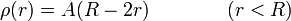
2 Introducción
La ley de Gauss establece que el flujo del campo eléctrico a través de una superficie cerrada es proporcional a la carga encerrada en su interior
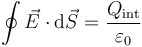
siendo  una constante universal conocida como permitividad del vacío.
una constante universal conocida como permitividad del vacío.
La ley de Gauss, aunque siempre es cierta, no siempre es útil como herramienta para hallar el campo eléctrico. La razón es que del valor de una integral definida no se deduce el valor del integrando (existen infinitas funciones diferentes que tienen la misma integral definida en un dominio dado).
Existe un caso, no obstante, en que la ley de Gauss permite obtener el campo eléctrico. Si la distribución de carga posee simetría esférica o de revolución, de manera que se ve igual desde todas las direcciones, el campo eléctrico que produce va en la dirección radial y depende solo de la distancia al centro de la distribución
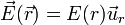
Este es el caso, por ejemplo, de una carga puntual.
Hay que remarcar que no todas las distribuciones de carga en una esfera poseen simetría esférica. Por ejemplo, una esfera cargada positivamente en su hemisferio “norte” y negativamente en el “sur” no posee simetría esférica, ya que no todas las direcciones son equivalentes. No se ve lo mismo desde el norte que desde el sur o desde el ecuador.
Suponiendo que sí existe simetría esférica, el flujo del campo eléctrico a través de una superficie esférica puede hallarse explícitamente. Si toamos una superficie esférica de radio r concéntrica con la distribución, el diferencial de superficie, ortogonal a ésta, va en la dirección radial
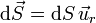
Por ello, el flujo se reduce a una integral de un escalar