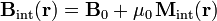Bobina larga con material ferromagnético (F2GIA)

De Laplace

Revisión de 11:33 25 abr 2012 (ver código fuente) Gabriel (Discusión | contribuciones) (→Permeabilidad relativa e imanación de la barra) ← Edición más antigua		Revisión de 11:34 25 abr 2012 (ver código fuente) Gabriel (Discusión | contribuciones) (→Permeabilidad relativa e imanación de la barra) Edición más nueva →
Línea 31:		Línea 31:
	Los ferromagnéticos son materiales que sometidos a la acción de un campo magnético, sufren un proceso de imanación: los momentos dipolares magnéticos que caracterizan macroscópicamente las propiedades mangéticas de sus átomos y moléculas, se orientan localmente en una dirección dominante, de manera que en cada punto del medio se pueden medir un momento dipolar magnético por unidad de volumen, <math>\mathbf{M}(P)</math>. Los diferentes valores de esta magnitud en el medio material, constituyen el campo de imanación.		Los ferromagnéticos son materiales que sometidos a la acción de un campo magnético, sufren un proceso de imanación: los momentos dipolares magnéticos que caracterizan macroscópicamente las propiedades mangéticas de sus átomos y moléculas, se orientan localmente en una dirección dominante, de manera que en cada punto del medio se pueden medir un momento dipolar magnético por unidad de volumen, <math>\mathbf{M}(P)</math>. Los diferentes valores de esta magnitud en el medio material, constituyen el campo de imanación.
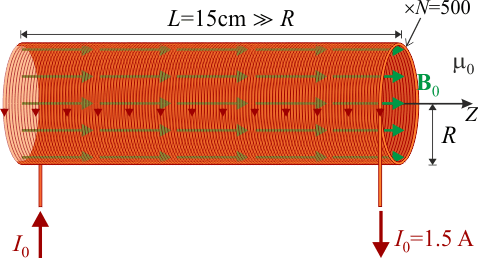
-	Si en el interior del solenoide, donde existe el campo <math>\mathbf{B}_0</math>, se coloca una barra de material ferromagnético, ésta se imanará. El campo de imanación resultante, <math>\mathbf{M}_\mathrm{int}(\mathbf{r})</math>,crea su propio campo magnético que se superpone al generado por la corriente <math>I_0</math>, de manera que el campo magnético total existente en el interior de medio magnético será:	+	[[Archivo:solenoide_2.gif|left]]Si en el interior del solenoide, donde existe el campo <math>\mathbf{B}_0</math>, se coloca una barra de material ferromagnético, ésta se imanará. El campo de imanación resultante, <math>\mathbf{M}_\mathrm{int}(\mathbf{r})</math>,crea su propio campo magnético que se superpone al generado por la corriente <math>I_0</math>, de manera que el campo magnético total existente en el interior de medio magnético será:
	<center><math>\mathbf{B}_\mathrm{int}(\mathbf{r})=\mathbf{B}_0+\mu_0\!\ \mathbf{M}_\mathrm{int}(\mathbf{r})</math></center>		<center><math>\mathbf{B}_\mathrm{int}(\mathbf{r})=\mathbf{B}_0+\mu_0\!\ \mathbf{M}_\mathrm{int}(\mathbf{r})</math></center>

---

Revisión de 11:34 25 abr 2012

Contenido 1 Enunciado 2 Solución 2.1 Campo en el interior del solenoide 2.2 Permeabilidad relativa e imanación de la barra

1 Enunciado

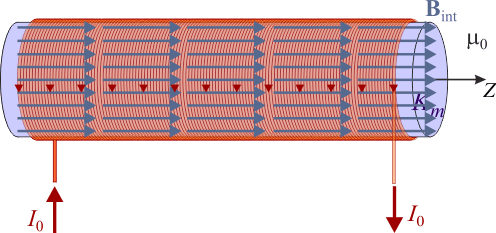
Se dispone de una bobina de 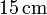de longitud y 500 vueltas que puede considerarse un solenoide largo. Se hace pasar por el solenoide una corriente de 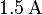y, a continuación, se introduce una barra de material ferromagnético en su interior. Al hacer esto se comprueba que el campo magnético en el interior del solenoide se ha multiplicado por 7000. Calcúlese:

1. Campo magnético en el interior del solenoide antes de introducir la barra ferromagnética.
2. Permeabilidad relativa y valor del campo de imanación en la barra ferromagnética.
3. El solenoide se utiliza para desimanar una barra imantada en su dirección longitudinal, que tiene un campo coercitivo 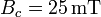. ¿Qué intensidad de corriente y en qué sentido debe circular por la bobina para anular el campo en su interior?

Datos: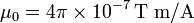

2 Solución

2.1 Campo en el interior del solenoide

Una bobina o solenoide se construye con un conductor filiforme enrollado sobre una superficie, no necesariamente cilíndrica, pero que mantiene una sección transversal constante, a lo largo de una dirección longitudinal. Para que constituya un solenoide, es necesario que las N vueltas del conductor se realicen de manera que den lugar a un N espiras idénticas, contenidas en planos prácticamente paralelos y distribuidos de forma continua. Esto es posible si el hilo conductor que forma la bobina tiene un espesor despreciable en relación con las dimensiones de la bobina, y el devanado o enrollamiento se realiza sin solución de continuidad (cada vuelta está en contacto con la previa y la posterior).

Cuando una corriente eléctrica estacionara recorre el conductor filiforme, en las N espiras del solenoide circula la misma intensidad de corriente. En el caso ideal de solenoide infinitamente largo con n espiras por unidad de longitud, una corriente eléctrica de intensidad I₀ recorriendo el solenoide (o lo que es lo mismo, cada una de las espiras), crea un campo magnético uniforme (constante en módulo ,dirección y sentido), pero sólo en el interior de la bobina:

 

siendo 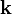el vector unitario en la dirección del eje de la bobina, es decir, la dirección perpendicular a los planos que contienen a las espiras o vuletas. El sentido de 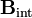queda determinado por el sentido en que la intensidad I₀ recorra las espiras, siguiendo el criterio “levógiro” o del triedro directo. El resultado anterior es también válido en solenoides largos cuya longitud L sea considerablemente mayor que las dimensiones de cada espira, y siempre que se evalue el campo lo suficientemente lejos de los extremos de la bobina como para que ésta pueda considerarse de longitud indefinida. Si el conducto filiforme es muy delgado y el enrollamiento se ha hecho adecuadamente, la densidad de espiras será la relación entre el número y la longitud en la que se distribuyen (longitud del solenoide). En el caso bajo estudio...

En consecuencia, la magnitud del campo magnético en el interior de la bobina (y no cerca de los extremos), cuando por ella circula una corriente estacionaria de 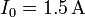es...

2.2 Permeabilidad relativa e imanación de la barra

Los ferromagnéticos son materiales que sometidos a la acción de un campo magnético, sufren un proceso de imanación: los momentos dipolares magnéticos que caracterizan macroscópicamente las propiedades mangéticas de sus átomos y moléculas, se orientan localmente en una dirección dominante, de manera que en cada punto del medio se pueden medir un momento dipolar magnético por unidad de volumen, 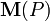. Los diferentes valores de esta magnitud en el medio material, constituyen el campo de imanación.

Si en el interior del solenoide, donde existe el campo , se coloca una barra de material ferromagnético, ésta se imanará. El campo de imanación resultante, 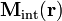,crea su propio campo magnético que se superpone al generado por la corriente I₀, de manera que el campo magnético total existente en el interior de medio magnético será: